5 Kalkulasjonsrenten
5.1 Innledning
Fra utvalgets mandat:
Størrelsen på kalkulasjonsrente har vesentlig innvirkning på lønnsomheten av langsiktige tiltak. Retningslinjene for fastsettelse av kalkulasjonsrente er basert på eksponentiell diskontering og den såkalte kapitalverdimodellen. Finansmarkeder gir imidlertid begrenset informasjon om risikopremier for prosjekter med lang levetid, som for eksempel samferdselsinvesteringer. Stern-rapporten har anbefalt en kalkulasjonsrente på 1,4 pst. for klimaberegninger, mens andre økonomer har hevdet at dette anslaget er for lavt. Gruppen skal på denne bakgrunn vurdere hvilken kalkulasjonsrente som bør legges til grunn for langsiktige tiltak, og om avkastningskravet bør differensieres etter tiltakenes virketid. Utvalget skal gå gjennom eksisterende litteratur på området, og vurdere ulike måter å fastsette kalkulasjonsrente på. Utvalget skal herunder vurdere om det teoretiske rammeverket for fastsettelse av kalkulasjonsrente bør ta utgangspunkt i kapitalens alternativkostnad eller i konsumentatferd. I et porteføljeperspektiv er det videre knyttet systematisk usikkerhet til både nytte- og kostnadssiden. Utvalget skal komme med en anbefaling om hvordan systematisk usikkerhet bør håndteres i offentlige investeringsanalyser.
De fleste offentlige tiltak har virkninger både på nytte- og kostnadssiden som strekker seg over flere år. For å vurdere tiltak må vi derfor kunne veie sammen samfunnsøkonomiske kostnader og nyttevirkninger som påløper på ulike tidspunkter. Samtidig er det betydelig usikkerhet knyttet til virkninger som kommer langt fram i tid. En samfunnsøkonomisk analyse bør også ta hensyn til slik usikkerhet.
I NOU 1997: 27 anbefales det at disse hensynene tas ved å benytte en kalkulasjonsrente som både fanger opp avveiningen mellom ulike perioder og konsekvensene av en usikker framtid for en beslutningstaker som helst vil unngå usikkerhet. Alternativt kan det benyttes en risikofri rente, mens det korrigeres for risiko i de usikre prosjektoverskuddene slik at kalkulasjonsrenten kun fanger opp avveiningen mellom ulike perioder.
Noen offentlige tiltak kan ha virkninger som strekker seg over svært lang tid. Dette kan for eksempel gjelde klimatiltak eller tiltak rettet inn mot biodiversitet. I NOU 2009: 16 drøftes usikkerhet og diskontering av slike tiltak nærmere.
I dette kapittelet ser vi først på ulike teoretiske tilnærminger til kalkulasjonsrente og drøfter håndtering av systematisk risiko (5.2). Deretter redegjør vi for retningslinjer for kalkulasjonsrenten i Norge (5.3) og går nærmere inn på teorier for hvordan kalkulasjonsrenten kan utvikle seg på særlig lang sikt (5.4). Vi vil så drøfte nivået på kalkulasjonsrenten (5.5), før vi går gjennom empiriske anslag for de samfunnsøkonomiske kalkulasjonsrenter som anvendes i en del andre land (5.6). Utvalgets vurderinger og tilrådinger presenteres i henholdsvis kapittel 5.7 og 5.8.
5.2 Kalkulasjonsrente
Diskontering ved bruk av kalkulasjonsrente regner fremtidige verdier om til kontantekvivalente verdier vurdert på et bestemt referansetidspunkt. For en investering velges vanligvis starttidspunktet for prosjektets fremtidige kostnader og inntekter som referansetidspunkt. Den kontantekvivalente verdien kalles da nåverdi. Diskontering muliggjør dermed sammenligning og rangering av tiltak med økonomiske virkninger som inntreffer på ulike tidspunkt.
Det er to innfallsvinkler til kalkulasjonsrentebegrepet. Det kan tolkes som et avkastningskrav i form av den minste økonomiske kompensasjon per krone investert som kreves for at en vil være villig til å avstå konsum nå mot å få et høyere konsum en periode senere. Det kan alternativt tolkes som en markedsbestemt alternativkostnad ved at det er det merkonsum en ville ha hatt etter en periode ved å plassere en krone i banken eller i annen rentebærende plassering i stedet for å konsumere den nå. Individets konsum- og spareprofil er optimal når individets subjektive avkastningskrav er lik alternativkostnaden gitt ved markedsrenten.
Usikkerhet som påvirker anslag på kalkulasjonsrenten kan deles inn i to kategorier. Det ene gjelder usikkerhet om utvikling i økonomien som sådan, noe som ikke ble drøftet i denne sammenheng i NOU 1997: 27. Her har vi både usikkerhet knyttet til fremtidig konsumutvikling som påvirker konsumentenes avkastningskrav, og vedrørende fremtidig alternativavkastning i kapitalmarkedet. Dette kan påvirke valg av diskonteringsrente til bruk i vurdering av offentlige prosjekter og eventuell tidsstruktur på en slik rente på særlig lang sikt. Dette drøftes nærmere i kapittel 5.4.
For det andre har vi usikkerhet om det økonomiske resultatet fra de prosjekter og tiltak som kapitalen bindes i. Dette er en usikkerhet som reflekteres i kalkulasjonsrenten i form av en prosjektspesifikk risikopremie. Dette er drøftet inngående i NOU 1997: 27 i lys av kapitalverdimodellen. I finanslitteraturen er det utviklet veletablerte modeller for prising av risiko knyttet til finansaktiva, herunder kapitalverdimodellen. De bygger imidlertid på forutsetninger som kan være problematiske for vurdering av risikopremier for langsiktige offentlige prosjekter. Dette diskuteres nærmere i kapittel 5.4.2.
Ulike teoretiske tilnærminger til hvordan kalkulasjonsrenter anslås, belyser ulike sider ved kalkulasjonsrenteproblemet. Vi ser først nærmere på en sentral modell for avkastningskravet til konsumenten i kapittel 5.2.1.
5.2.1 Avkastningskravet til konsumenten
En investering er lønnsom hvis den framtidige avkastningen, vurdert fra i dag, anses som mer verdt enn nyttetapet ved å oppgi konsum i dag. En enkel tilnærming til slike lønnsomhetsvurderinger er at de påvirkes av avkastningen på investeringen, utålmodigheten til den som investerer og i hvor stor grad konsumenten, stilt overfor en ujevn tidsprofil for livsinntekt, foretrekker konsumutjevning over tid.
Hvis vi antar at dette danner rammene for beslutningene til en representativ konsument, får vi et uttrykk for marginalbetingelsen for optimal sparing i en situasjon uten usikkerhet verken om prosjektets avkastning eller om utviklingen i økonomien for øvrig. Utålmodighet kan uttrykkes som en tidspreferanserate som sier hvor mye en nytteenhet skal justeres i forhold til hvor langt den ligger ut i tid. Jo mer utålmodig konsumenten er, jo høyere er tidspreferanseraten. Preferanse for konsumutjevning kan uttrykkes ved grensenytteelastisiteten som viser prosentvis endring i grensenytte når konsumet endres med én prosent. Jo høyere tallverdi på grensenytteelastisiteten, desto større ønske om konsumutjevning over tid. Videre kan vi se på den endringen i konsum som vi har fra en periode til den neste, som resultat av økonomisk vekst. Med dette utgangspunktet kan vi utlede den såkalte Ramsey-betingelsen for optimal sparing
(1)r = p + µg
der r står for avkastningen på investeringer, p er konsumentens tidspreferanserate, g er relativ konsumvekst per capita, og µ er tallverdien av grensenytteelastisiteten.1 Produktet µg viser prosentvis endring i grensenytte når konsumet endres med g prosent. Når en også inkluderer tidspreferanseraten, uttrykker dermed høyresiden av (1) det konsumbaserte avkastningskravet. Dersom for eksempel µ = 2 og fremtidig konsum øker (reduseres) med 1,5 prosent, vil avkastningskravet på sparing øke (reduseres) med 3 prosentpoeng.
Med økonomisk vekst vil befolkningen ha det materielt sett bedre i framtiden enn i dag; noe som vil manifestere seg ved en økning i konsum per capita. Dette fører i henhold til optimumsbetingelsen (1) til et høyere avkastningskrav. Et høyere avkastningskrav betyr at en legger relativt større vekt på konsum i dag fremfor å få realisert mer konsum senere. Med en høy diskonteringsrente vil et prosjekt da være lønnsomt bare i de tilfeller det gir en relativt høy avkastning i senere perioder. Et fallende per capita konsum – for eksempel som følge av sterk befolkningsvekst – vil på tilsvarende måte føre til et lavere avkastningskrav og større insentiv til sparing. På denne måten vil det siste leddet i avkastningskravet gitt ved (1) føre til konsumutjevning over tid.2 Det er rimelig å kalle dette leddet en velstandseffekt. En formodning om en vedvarende stigende (fallende) velstandsutvikling i et generasjonsperspektiv burde da nedfelle seg i en økende (fallende) kalkulasjonsrente over tid for prosjekter med tilsvarende langsiktige virkninger.
Det er rimelig at det er en sammenheng mellom hvordan konsum fordeles mellom rike og fattige på et gitt tidspunkt og mellom fattige og rike på ulike tidspunkt. Det er imidlertid ikke gitt at grensenytteelastisiteten er den samme i de to problemstillingene, siden fordeling på et gitt tidspunkt nødvendigvis gjelder fordeling mellom ulike individer, mens fordeling over tid kan gjelde fordeling mellom ”deg selv i dag” og ”deg selv i framtiden” (se Atkinson mfl. 2009 for en empirisk undersøkelse av hvordan disse kan variere)3. Som anslag på en kalkulasjonsrente til bruk i samfunnsøkonomiske analyser kan en legge til grunn en kontinuerlig positiv økonomisk vekst og identifisere sannsynlige verdier for de ulike parametrene i Ramsey-betingelsen (likning 1). Ulike anslag og forutsetninger om parameterverdiene som inngår i Ramsey-betingelsen, kan imidlertid gi svært ulike anslag på avkastningskravet. Harrison (2010) viser at ulike kilder kommer fram til avkastningskrav som varierer mellom 1,4 prosent og 8 prosent, jf. tabell 5.1 som gir en oversikt over kalkulasjonsrenter til bruk både for marginale tiltak og for klimaspørsmålet globalt (for eksempel Stern, 2007 og Cline, 1993). Dette illustrerer at det ikke er noe enkelt svar på hva en riktig diskonteringsrente er ved bruk av denne enkle tilnærmingen, selv før man introduserer spørsmålet om usikkerhet i hhv. prosjektets avkastning som drøftes i 5.2.2. og usikkerhet om alternativavkastningen på lang sikt som drøftes i kapittel 5.3. Boks 5.1 illustrerer hvordan valg av diskonteringsrente har vært sentralt i klimadebatten.
Tabell 5.1 Ulike samfunnsøkonomiske diskonteringsrenter utledet av Ramsey-betingelsen
Source | Pure rate of sosial time preference, θ | Elasticiti of marginal utility of consumption, η | Growth rate in consumption, g) | Discount rate = θ + ηg |
|---|---|---|---|---|
per cent | per cent | per cent | ||
Stern (2007) | 0.1 | 1 | 1.3 | 1.4 |
Quiggin (2006) | 0 | 1 | 1.5 | 1.5 |
Cline (1993) | 0 | 1.5 | 1 | 1.5 |
Garnaut (2008) | 0 | 1-2 | 1.3 | 1.3-2.6 |
HM Treasury (2003) | 1.5 | 1 | 2 | 3.5 |
Nordhaus (2007) | 1.5 | 2 | 2 | 5.5 |
Weitzman (2007) | 2 | 2 | 2 | 6 |
Arrow (2007) | 0 | 2-3 | lf 1-2 | 2-6 |
Dasgupta (2006) | 0 | 2-4 | lf 1-2 | 2-8 |
Gollier (2006) | 0 | 2-4 | lf 1.3 | 2.6-5.2 |
Empirical evidence | 0-3 | 0.2-4 | 1.2-2.1 (for Australia) | 0.24-11 (given range) |
Tabellen viser en oversikt over ulike samfunnsøkonomiske diskonteringsrenter som har fremkommet i ulike studier. Tabellen gir en oversikt over kalkulasjonsrenter til bruk både for marginale tiltak og for klimaspørsmålet globalt (for eksempel Stern 2007 og Cline, 1993).
Kilde: Harrison (2010), s. 36.
Boks 5.1 Kalkulasjonsrenten og klimaspørsmålet – et eksempel
Tiltak rettet mot å påvirke det globale klimaet må analyseres over en svært lang tidshorisont. Kalkulasjonsrenten blir da svært sentral for lønnsomhetsvurderinger. Dette har særlig vært drøftet i lys av den konsumbaserte tilnærmingen til kalkulasjonsrenten (jf. Ramsey-betingelsen, kapittel 5.2.1):
r = p + µg
Diskusjonen som framgår av Stern-rapporten om klimaproblemet (Stern, 2007) og et tilsvar til denne rapporten (Nordhaus, 2007a), illustrerer sentrale problemstillinger ved valg av en langsiktig diskonteringsrente. Stern (2007) setter den rene tidspreferanserate, p, til nær null ut fra en etisk vurdering om at nytten for fremtidige generasjoner skal veie like mye som for nåværende generasjoner i de intertemporale avveiningene.
Stern (2007) benytter også en lav verdi på µ. Det innebærer at det forutsettes lav preferanse for konsumutjevning over tid ved at det legges lite vekt på at framtidige generasjoner forventes å bli rikere enn dagens generasjoner. En høyere verdi på µ ville trukket i retning av at dagens generasjon burde spare mindre til framtidige generasjoner.
I Nordhaus (2007a) framheves det at avkastningen på alternative investeringer i markedet bør være retningsgivende for klimainvesteringer. Dette for å sikre en effektiv allokering av kapital i økonomien, på tvers av sektorer. I Nordhaus (2007a) legges det således vekt på at parameterverdiene i Ramsey-betingelsen bør være slik at kalkulasjonsrenten blir på nivå med observerbare markedsrenter. I Nordhaus (2007a) påpekes det at Sterns valg av kalkulasjonsrente innebærer at investeringsbeslutninger som fattes på grunnlag av beregninger med en slik rente vil føre til at det investeres for mye for tidlig i klimatiltak som har liten avkastning sammenlignet med de beslutningene som ville blitt truffet med en kalkulasjonsrente på nivå med observerbare markedsrenter. Ifølge Nordhaus (2007a) er en mer effektiv strategi å investere mer i konvensjonell kapital i en tidlig fase og deretter bruke avkastningen på disse investeringene til å investere betydelig i klimatiltak senere, noe som er konsistent med å benytte markedsrente som kalkulasjonsrente også for klimatiltak. Hvis man er bekymret for å overstige mulige terskelverdier i naturen, slik som at Grønlandsisen skulle smelte eller at ismassene i Vest-Antarktis skulle desintegrere, viser Nordhaus (2007b) videre til at det i økonomiske analyser av klimaspørsmålet kan innføres skranker på hvor store temperaturøkninger/karbondioksidkonsentrasjoner som skal tillates. Slike skranker kan innføres i analysene uten å endre valget av kalkulasjonsrente.
5.2.2 Markedsbasert alternativavkastning
Bruk av knappe ressurser til et bestemt formål innebærer en samfunnsøkonomisk kostnad ved at det fortrenger den potensielle verdiskapingen ved beste alternative anvendelse. Dette blir gjerne kalt alternativkostnaden. Dette gjelder også for kapitalbruk. Når kapital bindes opp i et bestemt prosjekt, vil dette gå på bekostning av alternativ lønnsom anvendelse. Kostnaden ved dette er den verdiskaping som går tapt ved det beste alternativet som blir valgt bort. I en økonomi uten kapitalrasjonering vil normalt alle prosjekter som gir en avkastning som er høyere enn kapitalens alternativavkastning i finansmarkedet bli realisert. Avkastningen i finansmarkedet blir da avkastningen på det marginale prosjektet, og markedsrenten blir bestemmende for etterspørselen etter kapital.
Samfunnet vil normalt stå overfor alternativer for anvendelsen av knappe ressurser, og kalkulasjonsrenten som alternativkostnad bør gi uttrykk for beste alternative avkastning for den kapital som bindes i et foreslått tiltak. I en lukket økonomi uten markedssvikt vil den realiserte markedsrenten i likevekt mellom tilbud og etterspørsel av kapital da uttrykke avkastningen på den beste alternative investeringen som vil være sammenfallende med avkastningskravet til konsumentene som vurderer om de skal spare eller konsumere i dag. I en åpen økonomi med et gitt internasjonalt rentenivå og frie kapitalbevegelser, tilpasser både tilbydere og etterspørrere av kapital seg til renten på verdensmarkedet, og denne renten vil definere alternativavkastning i finansmarkedet og avkastningskravet hos tilbydere av kapital.4 Denne vil da være den relevante kalkulasjonsprisen for avveining mellom konsum i ulike perioder. Mulighetene for avvik mellom avkastningskravet til konsumentene, den marginale reelle kapitalavkastningen og renten må være knyttet til imperfeksjoner i økonomien, for eksempel i form av vridende skatter. I NOU 1997: 27 drøftes slike imperfeksjoner i kapitalmarkedet nærmere.
Den praktiske anvendelsen av alternativkostnad som prinsipp i norsk sammenheng har vært at diskonteringsrenten for et prosjekt bygges opp av to elementer. For det første må alle prosjekter ha en avkastning som er minst like høy som en antatt sikker avkastning i internasjonale kapitalmarkeder. For det andre får diskonteringsrenten et tillegg som reflekterer den antatte risikoen ved prosjektet. Dette har da blitt brukt som uttrykk for risikojustert alternativavkastning i finansmarkedet for et offentlig prosjekt med antatt samme prosjektrisiko. Modeller for slik prising av risiko presenteres i kapittel 5.2.3 nedenfor. I kapittel 5.4 vil vi se nærmere på forholdet mellom usikkerhet på særlig lang sikt og den relevante kalkulasjonsrenten.
5.2.3 Modeller for prising av usikre finansielle fordringer
Finanslitteraturen er opptatt av hvordan investorer bør sette sammen sine porteføljer når avkastningen på framtidige fordringer er usikre. Modellene er i utgangspunktet basert på at investorer maksimerer forventet nytte av konsum. Veletablerte modeller, som for eksempel kapitalverdimodellen, knyttes imidlertid direkte opp mot priser og avkastning i markedet. Det gjør dem praktisk anvendelige, men krever også flere forenklede forutsetninger som kan være problematiske for offentlige prosjekter.
Hvis vi legger til grunn standardantagelsene om at økonomien består av rasjonelle investorer som kan foreta marginale investeringer, kan vi utlede en grunnleggende prisingsmodell for alle typer usikre finansielle fordringer. Boks 5.2 gir en nærmere gjennomgang av modellen.5
Boks 5.2 Grunnleggende prisingsmodell for alle typer usikre finansielle fordringer
La Pt være prisen på en usikker fordring på tidspunkt t, C være konsum, X være kontantstrøm og p være et uttrykk for investorers rene tidspreferanse. Maksimering av forventet nytte, gitt en budsjettrestriksjon, gir førsteordensbetingelsen:
PtU’(Ct) = Et[pU’(Ct+1)Xt+1]
Førsteordensbetingelsen sier at grensekostnaden for å kjøpe en enhet av fordringen må være lik forventet grensenytte av å eie en enhet av fordringen i neste periode. Hvis vi løser ligningen for P får vi den grunnleggende prisingsmodellen:
M kalles ofte for den stokastiske diskonteringsfaktoren. Modellen sier at prisen på en usikker framtidig fordring er lik den forventede neddiskonterte kontantstrømmen fra fordringen, der neddiskonteringen tar hensyn til intertemporal substitusjon, risikopreferanser og tidspreferanser (uttrykt ved marginalnytte og ρ). Investorer foretrekker fordringer som gir høy avkastning i de tilstandene og på de tidspunktene de har relativt lavt konsum og dermed relativt høy marginalnytte av en økning i konsumet (dårlige tider). Det vil drive opp prisene på disse fordringene. Omvendt vil prisene på fordringer som gjør det bra i gode tilstander eller i gode tider (og dårlig i dårlige tilstander eller dårlige tider) drives ned.
For å komme fra den generelle modellen til en modell som er praktisk anvendelig må vi spesifisere egenskapene til den stokastiske diskonteringsfaktoren. Vi må også komme rundt problemet med at det er vanskelig å finne gode konsumdata. Ulike forutsetninger og forenklinger av modellen gir opphav til mange av de prismodellene vi kjenner fra litteraturen, herunder kapitalverdimodellen og andre faktormodeller som ICAPM (Intertemporal Capital Asset Pricing Model) og Fama French-modellen.
Faktormodellene løser problemet med dårlige konsumdata ved å erstatte konsum med en eller flere andre faktorer som antas å representere konsum på en god måte, og som det finnes bedre data for. I tillegg antar man at forholdet mellom investorenes marginalnytte og faktorene er lineært.
Kapitalverdimodellen er en slik prismodell som er en likevektsmodell der aktørenes konsum knyttes opp til en eneste portefølje bestående av all formue i økonomien (markedsporteføljen). Modellen uttrykkes normalt på avkastningsform:
E(Ri) = r + ß(E(RM) – r)
der E(Ri) er forventet avkastning på et verdipapir i, r er risikofri rente, E(RM) er forventet avkastning på markedsporteføljen, og ß angir i hvilken grad investeringens avkastning samvarierer med avkastningen på markedsporteføljen. Modellen sier at investorer vil kreve en høyere risikokompensasjon desto mer avkastningen på et aktivum samvarierer med avkastningen på markedsporteføljen.
Det sentrale budskapet i modellen er at det er kun risiko som ikke kan diversifiseres bort ved å eie flere verdipapirer som prises i markedet. Dette kalles systematisk risiko. Man kan ikke oppnå en forventet avkastning som er høyere enn den risikofrie renten uten å påta seg systematisk risiko. Boks 5.3 gir en nærmere drøfting av skillet mellom systematisk og usystematisk risiko.
Boks 5.3 Systematisk og usystematisk risiko
Usikkerhet i et prosjekt kan deles opp i henholdsvis systematisk og usystematisk risiko. Risiko som avhenger av prosjektspesifikke forhold betegnes som usystematisk risiko. Dette kan f. eks. gjelde usikkerheten knyttet til geologien i et fjell det skal bores i for å bygge en tunnel. Også i andre prosjekter vil vi ha usikre kostnader som bare avhenger av prosjektspesifikke forhold. I noen av disse prosjektene vil de faktiske kostnadene bli lavere enn planlagt, mens de i andre vil bli høyere. Siden det i utgangspunktet ikke er noen samvariasjon mellom kostnadene i de ulike prosjektene, vil imidlertid utfallene av denne typen usikkerhet jevne seg ut når vi betrakter porteføljen av prosjekter for samfunnet som helhet. Vi sier at den usystematiske risikoen kan diversifiseres bort, og dette gjør at vi for denne typen risiko ikke skal øke avkastningskravet til et tiltak.
Med systematisk risiko derimot menes i hvilken grad gevinstene av tiltaket er følsomme for svingninger i marginalnytten av konsum. Videre kan en anta at marginalnytten av konsum er lavere når man blir rikere. En kan for eksempel tenke seg at avkastningen på en samferdselsinvestering varierer med konjunkturutviklingen. Nyttevirkningene av samferdselstiltak består i all hovedsak av redusert reisetid og økt sikkerhet. Dette utvalget anbefaler at både verdien av tid og statistisk liv skal realinntektsjusteres, og at anslag på vekst i BNP per capita skal benyttes som anslag på denne veksten, jf. drøfting i kapittel 4 om realprisjustering. En konsekvens av dette er at nyttesiden av samferdselsprosjekter i større grad enn tidligere samvarierer med avkastningen på nasjonalformuen og således framstår som tiltak med høyere systematisk risiko enn uten slik realinntektsjustering. Også verdiene av andre tiltak i samfunnet kan være konjunkturfølsomme. I tillegg vil det være andre tiltak, for eksempel innen eldreomsorg eller kriminalomsorgen som vil ha en samfunnsøkonomisk avkastning som ikke kan antas å være konjunkturfølsomme. I praksis vil det selvsagt være store gråsoner når man skal klassifisere konkrete usikkerhetselementer som enten systematiske eller usystematiske.
Ved tilstedeværelse av systematisk risiko må det i den samfunnsøkonomiske lønnsomhetsberegningen korrigeres for denne type usikkerhet. I dette kapittelet pekes det på hvordan det kan gjøres ved hjelp av et risikotillegg i kalkulasjonsrenten. Størrelsen på risikotillegget skal da i teorien avhenge av graden av samvariasjon mellom prosjektavkastningen og marginalnytten av konsum. Samfunnsøkonomisk avkastning av prissatte elementer består av nytte-elementer minus kostnadselementer. Positiv samvariasjon mellom prosjektets netto nytte og økonomien for øvrig øker risikoen mens positiv samvariasjon mellom netto kostnad og økonomien for øvrig reduserer risikoen. Begge tilfelle taler for et tillegg i diskonteringsrenten som reduserer nåverdien av netto nytte (lavere lønnsomhet) og reduserer nåverdien av netto kostnad (økt lønnsomhet).
En annen og mer direkte fremgangsmåte for å ta hensyn til risikoaversjon i beregningene, er å beregne de såkalte sikkerhetsekvivalente verdiene av de ulike nytte- og kostnadsverdiene på ulike tidspunkter, og benytte den risikofrie renten til diskontering. Det er her er tale om sikkerhetsekvivalente prosjektoverskudd som ved risikoaversjon vil være lavere enn forventet overskudd, hvis prosjektoverskuddet er positivt korrelert med avkastningen på nasjonalformuen. I teorien skal disse to tilnærminger være ekvivalente. I praksis krever utarbeidelse av sikkerhetsekvivalente nytte- og kostnadsverdier stor kjennskap til det enkelte elementet som verdsettes, og fastsettelsen innebærer også at det må gjøres flere antakelser. Samlet kan dette innebære at tilnærmingen som medfører bruk av sikkerhetsekvivalente nytte- og kostnadsverdier likevel kan være lite transparent og vanskelig å gjennomføre i praksis.
Kapitalverdimodellen har hatt stor betydning siden den ble utviklet på midten av 1960-tallet av Sharpe (1964), Lintner (1965) og Mossin (1966). Dette skyldes ikke minst at man med utgangspunkt i avkastningstall fra markedet kan bruke modellen til å anslå den gjennomsnittlige risikopremien i aksjemarkedet. Modellen egner seg derfor godt til alternativkostnadsvurderinger. Dersom man har et prosjekt som skal finansieres, og man har anslag på hvor stor prosjektrisikoen er i forhold til et gjennomsnittlig prosjekt som finansieres på børsen (β), kan man få et anslag på alternativavkastningen i finansmarkedet for prosjektet. Modellen har også vært benyttet for å tilnærme seg hva som er den relevante alternativavkastningen i finansmarkedet for et offentlig prosjekt, og på den måten anslå hva som er en rimelig kalkulasjonsrente for offentlige tiltak. Finansdepartementet (2005) gir en mer teknisk gjennomgang av en slik tilnærming.
Kapitalverdimodellen gir en enkel og pedagogisk fremstilling av viktige prinsipper for formuesforvaltning og er en veletablert modell for prising av risikable prosjekter. Modellen bygger imidlertid på flere forenklede forutsetninger. De to viktigste er at investorene bare lever i en periode og at de ikke har noen form for arbeidsinntekter i denne perioden. Videre innebærer antakelsen om et lineært forhold mellom marginalnytte og avkastningen på markedsporteføljen enten at investorene har såkalte forventningsvarians-preferanser eller at avkastningen på alle aktiva er normalfordelt.6 Modellen antar også at det finnes en investerbar markedsportefølje bestående av all formue i økonomien. Som det pekes på i Meld. St. 17 (2011-2012), boks 2.10, tyder empirisk forskning på at modellen ikke gir noen fullgod beskrivelse verken av hvordan investorene opptrer eller av hvordan finansmarkedene virker. Forskningen gir for eksempel klare indikasjoner på at systematiske deler av avkastningen på aksjer blir bestemt av flere faktorer enn beta (Banz, 1981, Fama og French, 1993, Jagadeesh og Titman, 1993).
Det vil normalt være usikkerhet knyttet til et prosjekts bidrag til samfunnsøkonomisk verdiskaping. Den systematiske usikkerheten for et offentlig prosjekt kan operasjonaliseres ved å ta hensyn til i hvor stor grad prosjektets avkastning samvarierer med avkastningen på nasjonalformuen, som typisk måles ved nasjonalinntekten. Uttrykket ”nasjonalinntekt” må da forstås i vid forstand, og skal i prinsippet inkludere alt som bidrar til landets velferd. Bruk av for eksempel Statistisk sentralbyrås mål på nasjonalinntekten vil således kun være en tilnærming til en slik teoretisk størrelse. Ved å anslå hvor usikker avkastningen er i forhold til et gjennomsnittlig privat prosjekt, kan prisingen av prosjektrisiko basert på kapitalverdimodellen gi oss et uttrykk for den samfunnsøkonomiske risikojusterte alternativavkastningen som prosjektet kan vurderes opp mot.
Det er imidlertid særlig to forhold som gjør det problematisk å bruke kapitalverdimodellen til å fastsette kalkulasjonsrenter for offentlige prosjekter. Det ene er at modellen i sin enkle form kun holder for én periode. Det andre er at modellen antar at alle formuesobjekter er omsettelige og har en markedspris, mens store deler av nasjonalformuen er uomsettelig.
I praksis er det vanlig å anta konstant risikofri rente og konstant risikopremie når prosjekter med løpende kontantstrømmer verdsettes ved hjelp av et avkastningskrav som er beregnet på grunnlag av en kapitalverdimodell ut fra markedsdata. Begge disse antakelsene kan være tvilsomme for offentlige prosjekter med lang investeringshorisont.
Over lengre tidshorisonter er det naturlig å anta at både renter, risikopremier og volatiliteter kan endre seg. Modellering av dynamiske konsum- og investeringsprosjekter er derfor komplisert. Problemet med usikkerhet over tid i den såkalt risikofrie renten tas opp senere i dette kapittelet. Den klassiske løsningen på et porteføljevalgsproblem over flere perioder, som Mossin (1968), Samuelson (1969) og Merton (1969) har hver sine versjoner av, er at investeringshorisonten under gitte forutsetninger er irrelevant for optimale porteføljevalg. En viktig forutsetning for irrelevansresultatet er at avkastningen på risikable aktiva er uavhengig og identisk fordelt over tid7. Hvordan avkastningen på risikable aktiva utvikler seg over tid er omdiskutert. Flere empiriske arbeider tyder imidlertid på at aksjeavkastning er ”mean reverting”, det vil si at avkastningene over tid tenderer til å komme tilbake til et gjennomsnitt dersom de av ulike årsaker avviker fra et slikt snitt på et gitt tidspunkt. En rasjonell forklaring på mean reversion er at risikopremier varierer over tid i takt med konjunktursyklene i økonomien.
Dersom kapitalverdimodellen like fullt skal benyttes som rammeverk for utarbeidelsen av en kalkulasjonsrente for offentlige tiltak, burde ideelt sett både anslag for risikopremien og beta være basert på nasjonalinntekten. I praksis er imidlertid alle prisdata fra de noterte egenkapitalmarkedene. Tall for nasjonalinntekten hentes fra nasjonalregnskapet og inneholder ingen informasjon om risikovurderinger. Det betyr at vi må tro at anslag på aksjepremien er en riktig pris på risikoen knyttet til offentlige prosjekter dersom disse skal benyttes i fastsettelse av en kalkulasjonsrente for offentlige tiltak. Det kan trolig forsvares ut fra en alternativkostnadstankegang, gitt at vi godtar at børsaktørenes risikoaversjon er noenlunde representativ for dem som bærer risikoen for offentlige prosjekter, jf. omtale i NOU 1997: 27. I tillegg må vi ha en metode for å anslå beta for offentlige prosjekter. Det er vanskelig fordi tall for netto nytte av et offentlig prosjekt - i motsetning til avkastningen på en aksje - ikke er lett tilgjengelig og basert på markedspriser.
Det finnes også modeller for å estimere beta på uomsettelige objekter, se Minken (2005). Slike beregninger er imidlertid nokså kompliserte, samtidig som datagrunnlaget er dårlig. Analysen i Minken (2005) viser at resultatene fra slike beregninger er svært følsomme for endringer i data.
5.3 Norske retningslinjer for valg av kalkulasjonsrente
5.3.1 Historiske retningslinjer
Fra 1967 til 1999 benyttet man i Norge en tilnærming der Ramsey-modellen lå til grunn for kalkulasjonsrenten. På bakgrunn av en utredning av Leif Johansen i 1967 hvor det antas at ρ = 1 prosent, µ = 3 og g = 3 prosent, ble kalkulasjonsrenten i rundskriv R-3/1975 fastsatt til 10 prosent. I rundskriv R-25/78 ble kalkulasjonsrenten endret til 7 prosent.
Ved revisjonen av rammeverket for samfunnsøkonomiske analyser i 1998 ble det ansett at forutsetningene om en liten åpen økonomi var rimelige for Norge. Risikofri rente og risikopremier ble ansett i større grad å bli bestemt fra internasjonale markeder. Den såkalte kapitalverdimodellen (se kapittel 5.2.2) ble da lagt til grunn for anslag på den relevante kalkulasjonsrenten.
Kapitalverdimodellen ligger til grunn for anbefalingene i NOU 1997: 27. I Finansdepartementets veiledere fra 2000 og fra 2005 er det redegjort nærmere for hvordan modellen kan tilpasses til å gi et uttrykk for en rimelig kalkulasjonsrente til bruk i samfunnsøkonomiske analyser. I rundskriv R-14/99 ble det fastsatt at man i samfunnsøkonomiske analyser skulle legge til grunn en risikofri realrente på 3,5 prosent. Det ble definert tre ulike risikoklasser, med risikojustert rente på hhv. 4, 6 og 8 prosent. For store prosjekter eller grupper av prosjekter ble det anbefalt en særskilt beregning av risikojustert avkastningskrav.
5.3.2 Dagens retningslinjer
Etter revisjon av Finansdepartementets veileder i samfunnsøkonomisk analyse i 2005 ble det sendt ut et nytt rundskriv R-109/2005 som erstattet R-14/99. Her ble risikofri rente til bruk i samfunnsøkonomiske analyser av statlige tiltak fastsatt til 2 prosent, og man pekte på at et normalprosjekt vil ha et risikopåslag på 2 prosentpoeng og dermed et risikojustert avkastningskrav på 4 prosent. For tiltak der det er rimelig å anta betydelig systematisk risiko, framgår det at et risikopåslag på 4 prosentpoeng og dermed en kalkulasjonsrente på 6 prosent kan være hensiktsmessig. Det stod fast at det for store prosjekter eller grupper av prosjekter ble anbefalt en særskilt beregning av risikojustert avkastningskrav. Dette gjelder særskilt for prosjekter som inngår i systemet for kvalitetssikring av store offentlige prosjekter (KS1), jf. omtale i kapittel 5.3.3 nedenfor.
Samferdselsdepartementet har initiert et prosjekt for å vurdere kalkulasjonsrenten nærmere for prosjekter innen sine ansvarsområder. Minken (2005) presenterer en analyse av samferdselsprosjekter i Norge der han tilrår en kalkulasjonsrente på 4,5 prosent for veg- og jernbaneprosjekter og 5 prosent for havner og flyplassinfrastruktur. Denne er bygget opp av et anslag på 2 prosent risikofri rente og et påslag for systematisk risiko på hhv. 2,5 prosent og 3 prosent. Minken (2005) peker imidlertid på at analysen er svært følsom for de data som inngår i analysen. Videre peker han på at manglende realprisjustering av enhetsprisene som avhenger av inntekt (særlig verdien av tid og liv) isolert sett kan tilsi en reduksjon i kalkulasjonsrenten som framkommer på 0,5 – 1 prosent. Samferdselsdepartementet konkluderte med å benytte en kalkulasjonsrente på 4,5 prosent for alle prosjekter innen sitt ansvarsområde, og av praktiske årsaker ikke å skille mellom veg, jernbane og luftfart.
5.3.3 Dagens retningslinjer for prosjekter som er omfattet av kvalitetssikringsregimet for store statlige investeringer
Regjeringen igangsatte høsten 1997 et prosjekt for å gjennomgå og foreslå forbedringer i systemene for å planlegge, gjennomføre og følge opp store statlige investeringsprosjekter. Kvalitetssikringsregimet omfatter nå både konseptvalget (KS1) og styringsunderlag samt kostnadsoverslag, herunder usikkerhetsanalyse av det valgte prosjektalternativet (KS2). Systemet for kvalitetssikring av store prosjekter gjelder for prosjekter med en anslått samlet investeringskostnad på over 750 mill. kroner (Finansdepartementet 2011).
KS1 gjelder kvalitetssikring av beslutningsunderlaget for å starte opp et forprosjekt. Konkret er det seks forhold som kvalitetssikres: en behovsanalyse, et overordnet strategidokument, et overordnet kravdokument, en mulighetsstudie, en alternativanalyse og føringer for forprosjektfasen. I alternativanalysen inngår samfunnsøkonomiske analyser av nullalternativet og minst to alternative hovedkonsepter. Det benyttes inngangsdata fra egne usikkerhetsanalyser, hvor det beregnes forventningsverdier og spredningsmål på de ulike usikkerhetselementene. Gjennom usikkerhetsanalysen tas det sikte på å beregne direkte den systematiske usikkerheten som er relevant for samfunnet. En får med seg blant annet forskjeller i systematisk usikkerhet knyttet til investeringsutgiften, variasjoner i nivået på den systematiske usikkerheten knyttet til nyttevirkningene og ikke minst variasjoner i hvordan usikkerheten i nytte løses opp over prosjektets levetid.
I dagens retningslinjer pekes det på at dette gir et sikrere uttrykk for den systematiske usikkerheten enn et sjablongmessig risikotillegg i kalkulasjonsrenten. Det generelle risikotillegget i kalkulasjonsrenten er på det grunnlaget ikke gjort gjeldende for prosjekter som faller innunder statens regler for ekstern kvalitetssikring. Som utgangspunkt for analysene har derfor den risikofrie kalkulasjonsrenten på 2 prosent vært benyttet, eventuelt justert for anslått systematisk risiko. Det har vist seg krevende å justere for systematisk risiko på denne måten, og kun i få tilfeller har det blitt anslått noen konkret risikojustering for de enkelte prosjekter. Resultatet har derfor blitt at mange store prosjekter kun er diskontert med risikofri rente på 2 prosent uten noen reell justering for systematisk usikkerhet gjennom risikopåslag eller sikkerhetsekvivalente verdier, mens små prosjekter (utenfor KS-ordningen) har forholdt seg til Finansdepartementets (2005) generelle anbefaling om 4 prosent rente for prosjekter med normal systematisk risiko (Vennemo, 2011).
5.4 Avveininger på særlig lang sikt i lys av usikkerhet
Utfordringen med å benytte markedsdata for å fastsette kalkulasjonsrenten er at de mest langsiktige rentebærende finansielle instrumenter som er gjenstand for handel, ikke har løpetider som samsvarer med levetiden på de aller mest langsiktige offentlige prosjektene. Hvordan usikkerhet utvikler seg og påvirker renten må derfor ta utgangspunkt i økonomisk teori. I kapittel 5.4.1 ser vi nærmere på usikkerhet om den generelle økonomiske utviklingen, og hvilke konsekvenser slik usikkerhet har for diskonteringsrenten og tidsstrukturen på denne. En ser da bort fra at det også kan være systematisk risiko i prosjektavkastningen. I kapittel 5.4.2 drøfter vi derimot sammenhengen mellom den systematiske usikkerhet ved prosjektets avkastning og diskonteringsrentens tidsutvikling. I kapittel 5.4.3 ses dette i lys av de globale miljøutfordringene slik det ble drøftet i NOU 2009: 16.
5.4.1 Usikkerhet om den generelle økonomiske utvikling
Samfunnsøkonomiske analyser av globale klimavirkemidler og klimatiltak nødvendiggjør analyser av virkninger svært langt fram i tid. Dette har initiert ny forskning om hvilken diskonteringsrente som er riktig å benytte på svært lang sikt.
Et sentralt moment som blir trukket fram, er den grunnleggende usikkerheten om framtidig global økonomisk utvikling. Felles for analysene av dette, er at det antas at konsumentene er risikoaverse. En tilnærming til å ta hensyn til usikkerhet om framtidig velstandsutvikling er å ta utgangspunkt i Ramsey-betingelsen, presentert i kapittel 5.2.1, og la økonomisk vekst være usikker. I Gollier (2008) presenteres for eksempel en slik utvidet Ramsey-betingelse der usikkerhet om framtidig økonomisk utvikling innebærer et forsikringsmotiv for sparing som tilsier lavere diskonteringsrente. Stilt overfor usikkerhet vil man, alt annet likt, investere noe mer for framtiden for å sikre seg i tilfelle av ugunstige fremtidige utfall knyttet til den enkeltes økonomiske situasjon. Under visse forutsetninger knyttet til preferanser og konsumets tidsutvikling innebærer tilnærmingen en stabil rente for alle år.8 Gitt forutsetningen om usikkerhet som tilsier stabil diskonteringsrente over tid, ser Gollier (2011) nærmere på størrelsen på forsiktighetselementet i avkastningskravet. For velstående land pekes det på at forsikringselementet er moderat som følge av en relativt stabil økonomisk vekst i disse landene. Gitt en forutsetning om grensenytteelastisitet på 2, som oppgis å være basert på skjønn, finner han for eksempel en rente for USA som reduseres fra om lag 3,5 prosent (dersom en ikke tar hensyn til usikkerheten) til 3,35 prosent (dersom man tar hensyn til denne). Dersom man derimot tar hensyn til den store variasjonen i inntekt globalt, finner han at forsiktighetselementet er langt større, og den globale renten skal da reduseres fra om lag 4,5 prosent til 0,7 prosent. Dette peker i retning av at i vurderingen av problemstillinger som berører hele planeten, for eksempel fastsettelsen av en global klimapolitikk, er det viktig å vurdere et slikt forsiktighetselement. Med andre forutsetninger – spesielt at det usikre konsumet er positivt korrelert over tid − viser Gollier (2008) at avkastningskravet er fallende over tid.9
Hvis man vurderer tiltak på særlig lang sikt, kan det også argumenteres for at det forventes at den økonomiske veksten vil være fallende over tid. Dette vil også isolert sett indikere en fallende rente over tid, jf. Ramsey-betingelsen med en fallende vekstrate i konsumet pr capita. Slike argumenter kan for eksempel knyttes til begrensede samlede globale ressurser og ved at økonomisk vekst i menneskehetens historie kun har vært normen de siste 250 år.
En annen tilnærming til usikkerhet om framtidig økonomisk utvikling, er modellert i Weitzman (1998) som usikkerhet om alternativavkastningen, uavhengig av usikkerhet om selve prosjektets avkastning. Her tas det utgangspunkt i kalkulasjonsrenten som en pris som reflekterer markedsbasert alternativavkastning, jf. kapittel 5.2.2. Dette reiser to spørsmål. Det ene er at når alternativavkastningen er usikker, må kalkulasjonsrenten være i form av en sikkerhetsekvivalent alternativavkastning. Dette reiser spørsmålet om sikkerhetsekvivalent rente i forhold til forventet rente.
Ved geometrisk diskontering blir nåverdien en konveks funksjon av diskonteringsrenten. Dette innebærer at usikkerhet om diskonteringsrenten fører til at forventet nåverdi av fremtidige prosjektoverskudd blir høyere enn nåverdien beregnet ut fra forventet rente (jf. den såkalte Jensens ulikhet). Følgelig blir den sikkerhetsekvivalente diskonteringsrenten lavere enn forventet rente. Den sikkerhetsekvivalente diskonteringsrenten blir implisitt bestemt ved forventningsverdien av diskonteringsfaktorene svarende til de usikre rentene, og ikke av forventningsverdien av rentene (jf. Weitzman, 1998 og Weitzman, 2012, boks 5.4).
For det andre har vi spørsmålet om tidsutviklingen for den sikkerhetsekvivalente renten. Denne tidsstrukturen avhenger av hvordan usikkerheten om alternativavkastningen endrer seg over tid. Newell og Pizer (2003) har en mer generell analyse av diskontering under usikkerhet basert på alternativavkastning der forutsetningene for tidsutviklingen av renten drøftes. Her pekes det på at tidsutviklingen av den sikkerhetsekvivalente renten avhenger av om man antar at den usikre framtidige renten tenderer tilbake mot et langsiktig gjennomsnitt (såkalt ”mean-reversion”) eller om man har positivt seriekorrelerte markedsrenter som følge av tilfeldige makroøkonomiske sjokk. I det første tilfellet har tilstedeværelse av usikkerhet relativt små konsekvenser for kalkulasjonsrenten. Den sikkerhetsekvivalente renten blir da med andre ord marginalt lavere enn den forventede renten. I det andre tilfellet vil den sikkerhetsekvivalente renten være betydelig lavere enn den forventede renten, særlig på lang sikt. Newell og Pizer (2003) ser på historisk renteutvikling av langsiktige statsobligasjoner i USA de siste 200 år, og estimerer på det grunnlag utviklingen i den sikkerhetsekvivalente renten. De finner at under antakelse om en renteutvikling basert på ”random walk”, vil stokastiske, makroøkonomiske sjokk med persistente virkninger implisere positivt seriekorrelerte renter. Dette fører til at den sikkerhetsekvivalente renten faller fra 4 prosent til 2 prosent etter 100 år, 1 prosent etter 200 år og 0,5 prosent etter 300 år. Dette er i tråd med tilnærmingen i Weitzman (1998). En modell som legger til grunn ”mean reversion” tilsier imidlertid at de samme historiske tallene innebærer en sikkerhetsekvivalent rente som i praksis er identisk med den forventede renten på 4 prosent de første 30-40 år, og som forblir høyere enn 3 prosent over de neste 200 år. Den faller til 1 prosent først etter 400 år. Newell og Pizer (2003) oppgir at bevis basert på standard statistiske tester ikke gir noe klart svar på hvilken modell som best beskriver data. Forfatterne peker likevel på at ”random walk” er den modellen som best beskriver data i de fleste forsøk på å dele det historiske datamaterialet i to perioder (såkalt ”split samples”), hvilket taler for en fallende rente over tid.
Hepburn mfl. (2009) tar i likhet med Newell og Pizer (2003) utgangspunkt i en analyse av variasjonen i historisk risikofri rente og ser på Australia, Canada, Tyskland og Storbritannia. Ulike spesifikasjoner av den økonometriske modellen gir noe ulike svar på tidsstrukturen for den langsiktige sikkerhetsekvivalente renten. Med utgangspunkt i en risikofri rente i år 1 på 3,5 prosent for Storbritannia, finner de for eksempel en rente som varierer mellom 3,54 prosent og 3,31 prosent etter 40 år og mellom 3,42 prosent og 3,22 prosent etter 100 år. I artikkelen pekes det på at det er størst empirisk belegg for modellen som gir det raskeste fallet i renten.
Snarere enn å forsøke å estimere en rente fra historiske data, viser Weitzman (2001) resultatene av en spørreundersøkelse blant et stort utvalg økonomer om hvilken reell diskonteringsrente som de mener er rimelig, ”alt tatt i betraktning”, for å vurdere et langsiktig klimaspørsmål. Gjennomsnittet i svarene er 4 prosent og standardavviket rundt 3 prosent. Weitzman (2001) benytter dette utvalget som en fordeling av mulige framtidige diskonteringsrenter, og i tråd med det mer generelle poenget i Weitzman (1998), viser han hvordan en slik spredning tilsier en fallende sikkerhetsekvivalent rente over tid. Ved å benytte funnene til å estimere en konkret fordeling for denne sikkerhetsekvivalente diskonteringsrenten, peker han på at dette, gitt hans tilnærming, tilsier en diskonteringsrente på 4 prosent de første fem år, deretter 3 prosent de neste 20 år, deretter 2 prosent de neste 50 år, 1 prosent fram til år 300 og deretter 0 prosent. Freeman og Groom (2012) peker imidlertid på at dette resultatet følger av en spesifikk antakelse om at respondentene i undersøkelsen oppga sitt svar som en normativ vurdering av hva de mente renten burde være, og ikke som et anslag på hva en gjennomsnittlig rente faktisk vil bli. Dersom respondentene faktisk oppga sine beste anslag på en gjennomsnittlig framtidig rente, er det fordelingen av individuelle gjennomsnittsanslag som er relevant, mens det ved den normative tolkningen er fordelingen til respondentenes normative anslag. I sistnevnte tilfelle vil variansen være betydelig større enn variansen til anslagene på fremtidig rente som vil være gitt ved spredningen til fordelingen av gjennomsnitt. Dersom en oppfatter svarene som den enkeltes beste anslag på fremtidig rente, vil det føre til en betydelig flatere terminstruktur for diskonteringsrenten enn det som følger av Weitzmans tilnærming. Siden det alltid vil være et element av normative svar, tilsier Freeman og Groom (2012) at Weitzmans resultater blir dempet, men at den fallende tendensen ikke blir helt fjernet.
Freeman og Groom (2012) peker på at det ikke er mulig å vite hva respondentene i Weitzman (2001) la til grunn for sine svar. Forfatterne peker på at ulik tolkning av svarene i stor grad gjenspeiler tilnærming til anbefaling om diskonteringsrente i Storbritannia, Frankrike og USA. Storbritannia og Frankrike har offentlige anbefalinger om en tidsstruktur på diskonteringsrenten som ligner den man får ut fra en normativ tolkning av respondentenes svar. Anbefalinger i USA derimot, med mindre dramatiske rentefall, ligner den man får med å tolke respondentenes svar som anslag på forventede gjennomsnitt.
Litteraturen gjennomgått ovenfor peker samlet sett på at økende usikkerhet om alternativavkastningen tilsier fallende kalkulasjonsrente. Årsaken er at det isolert sett blir mer attraktivt å realisere prosjektet ettersom usikkerheten rundt alternativavkastningen øker. Dette gir et lavere avkastningskrav og dermed en lavere kalkulasjonsrente. Litteraturgjennomgangen i dette kapittelet har vist at det er støtte for at usikkerheten om den makroøkonomiske utviklingen - og dermed alternativavkastningen - er stigende på særlig lang sikt, utover den perioden man med rimelighet kan sikre seg i finansmarkedene. Denne litteraturen tilsier således at kalkulasjonsrenten, vurdert fra analysetidspunktet, vil være fallende med tiden.
Såkalt hyperbolsk diskontering, eller nåtidsskjevhet, er også trukket fram som argument for en fallende kalkulasjonsrente over tid. (Harstad 2012). Hyperbolsk diskontering innebærer at folks grad av utålmodighet ikke er konstant, og at øyeblikket tillegges relativt sett større vekt enn det eksponentiell diskontering med konstant rente skulle tilsi. Det betyr at avveiningen mellom nytte i etterfølgende perioder endrer seg etter som tiden går. Dette fører til dynamisk tidsinkonsistens, som impliserer at lønnsomheten av en beslutning blir avhengig av når beslutningen fattes, til tross for at informasjonsgrunnlaget for beslutningen er uendret. En rekke empiriske undersøkelser viser imidlertid at nåtidsskjevhet er vanlig hos enkeltindivider, og dermed må antas å påvirke befolkningens betalingsvillighet for konsekvenser fram i tid. For nærmere diskusjon, se for eksempel Laibson (1997), Frederick mfl. (2002), Dasgupta og Maskin (2005).
5.4.2 Usikkerhet om tiltakets avkastning
Kapittel 5.4.1 handler om hvordan usikkerhet om den generelle økonomiske utviklingen påvirker hvilken risikofri rente som skal legges til grunn. Her finnes det en relativt omfattende litteratur. Et annet spørsmål er hvordan usikkerhet om selve prosjektets avkastning vil påvirke kalkulasjonsrenten på lang sikt. Dette vil i så tilfelle påvirke risikopåslaget i kalkulasjonsrenten, jf. kapittel 5.2.3 Modeller for prising av risiko og tilhørende faktabokser. Det foreligger en mer begrenset litteratur om den svært langsiktige tidsstrukturen for slike risikopåslag.
En teoretisk tilnærming til problemet er Weitzman (2012). På grunnlag av en konsumbasert flerperiodisk versjon av kapitalverdimodellen der netto konsum fra prosjektet består av en usystematisk komponent pluss en systematisk komponent som varierer proporsjonalt med det usikre totalkonsumet i økonomien med en faktor lik 0 ≤ß ≤1, utledes optimal diskonteringsrente. Den er implisitt gitt ved den risikojustert renten svarende til en diskonteringsfaktor som er et ß-veid gjennomsnitt av diskonteringsfaktoren kalkulert med den sikre renten og diskonteringsfaktoren kalkulert med den forventede avkastningen på den kapitalporteføljen som står bak verdiskapingen svarende til den usikre konsumkomponenten. Den én-periodiske versjonen av denne modellen gir et risikojustert avkastningskrav som er sammenfallende med avkastningskravet fra kapitalverdimodellen. Videre for enhver ß mellom 0 og 1 vil det risikojusterte avkastningskravet være fallende med tidshorisonten og går mot den sikre renten når horisonten blir tilstrekkelig lang.
Den verden som betraktes her, er genuint usikker. Over tid vil ethvert prosjekt som har en avkastning med en lavere usikkerhet enn verdiskapingen i den risikoutsatte delen av økonomien være en form for forsikring i det langsiktige perspektivet. For slike prosjekter blir derfor den usystematiske delen av verdiskapingen viktigere og viktigere over tid, mens den komponenten som er utsatt for systematiske risiko ”diskonterer seg selv ut”. Derfor skal kalkulasjonsrenten for prosjekter med en viss systematisk risiko falle over tid, ifølge Weitzman (2012). Prosjekter uten systematisk risiko vil i tråd med teorien ha rente konstant lik risikofri rente. Modellen til Weitzman (2012) er nærmere presentert i boks 5.4.
Kalkulasjonsrenten som anvendes til vurdering av offentlige prosjekter må vurderes ut fra summen av risikofri rente og det relevante risikopåslaget. Ulike modelltilnærminger har imidlertid det til felles at økende usikkerhet over tid knyttet til alternativavkastning impliserer et fallende risikojustert avkastningskrav.
Det har tidligere ikke vært vanlig å anvende en rente som varierer over tid i samfunnsøkonomiske analyser. Det er derfor verdt å presisere to forhold. For det første er bakgrunnen for fallende rente, slik det er presentert ovenfor, økende usikkerhet over tid. I en utredningssituasjon der en slik fallende rente skal anvendes, vil det derfor være riktig å legge til grunn at rentestrukturen vil gjelde fra analysetidspunktet. For det andre skal verdier i samme periode diskonteres ned med samme diskonteringsrente siden de er utsatt for den samme makroøkonomiske usikkerhet. Sett at en fallende kalkulasjonsrente operasjonaliseres med én rente de første 40 år og en lavere rente for årene deretter. Da skal en virkning i år 50 først diskonteres ned til år 40 med den lave renten, og videre derfra med den mer kortsiktige renten. Det er med andre ord ikke snakk om at en virkning kan endre verdi vesentlig ved å flyttes fra år 40 til år 41 eller lignende.
Boks 5.4 Sammendrag av Martin Weitzman (2012): Om risikokorrigerte diskonteringsrenter for offentlige investeringer
På grunnlag av velferdsvirkningene fra et postulert marginalt investeringsprosjekt evaluert innenfor rammen av en svært enkel dynamisk og stokastisk generell likevektsmodell, utledes den optimale risikojusterte diskonteringsraten for prosjektets netto konsumstrøm over tid. Det betyr at investeringen vil bidra til økt økonomisk velferd hvis og bare hvis nåverdien av kostnadene er mindre enn forventet nåverdi av konsumnytten kalkulert med disse diskonteringsrentene.
Preferansene for konsum er karakterisert ved konstant relativ risikoaversjon som er gitt ved grensenytteelastisiteten. Denne preferansestrukturen gjør det mulig å forenkle allokeringsproblemet ved at en kan se på investeringsmulighetene som bestående av to realaktiva; ett risikofritt aktivum som gir en konsumenhet i hver periode, og ett risikobetont aktivum, som kan tolkes som egenkapital, og som gir et utbytte i form av konsum som en fast andel av all løpende verdiskaping gitt ved totalkonsumet.
Netto nytte fra investeringen er en tilfeldig variabel som antas å bestå av to komponenter, og er gitt ved
I (1) står Ct for totalt konsum i økonomien på tidspunkt 1, ßter den komponenten av prosjektets bidrag til verdiskapingen som har samme risikoprofil som totalkonsumet, mens andelen 1 - ßter stokastisk uavhengig av verdiskapingen gitt ved totalkonsumet. Uten tap av generalitet kan dermed den siste komponent normaliseres ved å sette E[It] =1. Dette impliserer at forventet netto nytte på tidspunkt t er gitt ved bt.
Den rollen som andelen ßt har i denne modellen, ligner på investerings-betaen i den statiske kapitalverdimodellen. Men i denne konteksten reflekterer beta på tidspunkt t korrelasjonen mellom prosjektets bidrag til netto nytte og totalkonsumet på tidspunkt t. Weitzman kaller den for prosjektets real-beta.
For å gjøre analysen håndterbar antas det at ßt= ß for alle t.
Forholdet mellom den sikre renten rf og brutto avkastningen på det risikofrie aktivumet er gitt ved rf= ln(Rf) ≡ ln(erf), og tilsvarende for re = lnE[Re], der re den forventede renten svarende til den risikable bruttoavkastningen Re= ere på egenkapitalen.
Vi ser på en investering på tidspunkt 0 som kun gir avkastning på tidspunkt t, og som er gitt ved uttrykket for Bt i (1). Vi definerer X som det konsumtapet på tidspunkt null som gjør konsumenten eksakt indifferent mellom å akseptere eller forkaste dette hypotetiske prosjektet. Den kritiske verdien på konsumtapet må da tilfredsstille betingelsen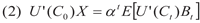
der a er en konstant som representerer den konstante tidspreferanseraten for nytte. Den korresponderende risikojusterte diskonteringsrenten må tilfredsstille betingelsen
Som følge av de forenklende egenskapene ved den iso-elastiske nyttefunksjonen kan den kritiske verdien på X utledes som
Innsetting for X fra (3) gir oss betingelsen (4) uttrykt ved diskonteringsfaktorer
Ved å ta den naturlige logaritmen på begge sider av (5) får vi den risikojusterte diskonteringsrenten gitt som
Dette betyr at den marginale investeringen vil bidra til økt velferd hvis og bare hvis forventet nåverdi av netto nytte diskontert med renten gitt ved (6) er positiv.
Sammenlignet med kapitalverdimodellen der risikojustert avkastningskrav er gitt ved et beta-veid gjennomsnitt av den risikofrie renten og forventet avkastning på markedsporteføljen, er den risikojusterte diskonteringsrenten i denne konsumbaserte investeringsmodellen implisitt gitt ved en optimal diskonteringsfaktor som er et beta-veid gjennomsnitt av henholdsvis diskonteringsfaktorene med den risikofrie renten og forventet avkastning på porteføljen av risikable aktiva. Det er derfor naturlig å se på betingelse (6) som en fler-periodisk generalisering av den statiske kapitalverdimodellen.
Den statiske varianten bygger på preferanser definert på forventning-varians, mens dens fler-periodiske motstykke bygger på konstant relativ risikoaversjon. Begge modellene innebærer imidlertid porteføljeseparasjon i likevekt, som gjør at vi kan se på totaløkonomien som bestående av to aktiva: ett aktivum med sikker avkastning og ett aggregat av alle aktiva i økonomien med risikofylt avkastning.
For t = 1 er diskonteringsrenten lik den beta-veide diskonteringsraten i kapitalverdimodellen, og går mot den risikofrie renten når t går mot uendelig. For enhver risikoprofil representert ved andelen 0 < ß < 1 av prosjektets avkastning som er perfekt korrelert med totalkonsumet i økonomien, vil den optimale diskonteringsrenten være fallende over tid og nærme seg den risikofrie renten som grenseverdi.
5.4.3 Diskontering og globale miljøutfordringer
I NOU 2009: 16 Globale miljøutfordringer – norsk politikk gis det en analyse av usikkerhet og diskontering, blant annet i lys av litteraturen ovenfor, på grunnlag av de bidrag som da forelå.
Det ble pekt på at det foreligger argumenter for at langsiktige klimatiltak skal vurderes med en lavere kalkulasjonsrente. Argumentene kan ifølge rapporten deles i to grupper. For det første er det usikkert om vi i tilstrekkelig grad tar hensyn til senere generasjoner dersom vi benytter en relativt høy diskonteringsrente også for langvarige prosjekter. For det andre kan vi være i tvil om informasjonen i observerbare markedsrenter er relevant også for senere perioder.
I rapporten ble problemstillingen illustrert ved å anta at både risikofrie renter og risikotillegg videre framover utvikler seg omtrent som vi kan anslå ut fra tilgjengelige markedsdata, og at det prosjektet vi betrakter, ikke er stort nok til å endre markedsprisene. Virkninger som kommer langt ut i tid, vil i så fall ha en svært lav nåverdi. Med en diskonteringsrente på 5 prosent vil for eksempel nåverdien av 1 krone om 50 år være 8,7 øre, og om 100 år bare 0,76 øre. Det ble pekt på at det på dette grunnlag ofte argumenteres med at prosjekter med virkninger langt ut i tid bør stå overfor en lav diskonteringsrente for å ta hensyn til framtidige generasjoner. NOU 2009: 16 pekte imidlertid på at det ikke er åpenbart at en lavere diskonteringsrente fanger opp det problemet vi ønsker å løse.
Det ble pekt på at gitt at det ikke i seg selv er et problem å verdsette alle inntekter og kostnader i kroner, bør vi på vanlig måte få fram i analysen hvilke grupper som tjener på prosjektet, og hvilke som taper på det. Hvis prosjektet har en negativ nåverdi når vi ikke tar hensyn til fordelingsvirkninger, mens de som ville tjene på prosjektet er framtidige generasjoner, har vi i utgangspunktet et fordelingsproblem og ikke et diskonteringsproblem. Den som utformer prosjektanalysen må i så fall få fram fordelingsvirkningene, og beslutningsfatter bør vurdere om prosjektet bør gjennomføres på grunn av de positive virkningene for framtidige generasjoner. I denne NOU-en drøftes fordelingsspørsmålet nærmere i kapittel 3.
I NOU 2009: 16 ble det videre pekt på at det for langsiktige prosjekter også er nødvendig å håndtere andre priser enn diskonteringsrenten på en riktig måte. Dersom for eksempel miljøgoder blir knappere over tid, er det grunn til å tro at verdien (kalkulasjonsprisen) på miljøgoder vil gå opp relativt til verdien på andre goder. Betydningen av slike endringer i relative priser kan ifølge NOU 2009: 16 være større enn betydningen av diskontering og gjøre at prosjekter blir samfunnsøkonomisk lønnsomme selv om inntektene kommer langt fram i tid. Dette utvalget drøfter realprisjustering nærmere i kapittel 4 og går spesifikt inn på realprisutviklingen til skyggeprisen for klimagassutslipp i kapittel 9. Det vises også til utvalget om verdsetting av biodiversitet som er nedsatt av Miljøverndepartementet.
NOU 2009: 16 tar så opp problemstillingen knyttet til å fastsette kalkulasjonsrente for perioder der vi ikke har observerbare markedspriser å støtte oss til. Her pekes det på at vi må vurdere hva som bestemmer risikofri rente og risikotillegg på lang sikt. Flere av modellene skissert ovenfor presenteres, og noen faktorer trekkes særlig fram: endret økonomisk vekst, endret usikkerhet, svakheter i datagrunnlag og markedssvikt.
NOU 2009: 16 konkluderte blant annet med at diskonteringsrenten i nytte-kostnadsanalyser bør være en realrente som er beregnet før skatt, og med en løpetid som er tilpasset prosjektlengden. Det bør i utgangspunktet benyttes markedsbaserte anslag for risikofri rente og risikotillegg. Det ble imidlertid pekt på at det er stor usikkerhet om anslagene for risikotillegg på lang sikt og til dels også for langsiktig, risikofri rente. NOU 2009: 16 foreslo ingen endringer i gjeldende praksis for fastsettelse av diskonteringsrente for offentlige prosjekter i Norge, samtidig som det ble pekt på at risikoen i mange offentlige prosjekter er lav.
5.5 Nivået på kalkulasjonsrenten
Ved å sammenligne renten som kreves for korte og lange lån, kan man få et inntrykk av hvordan markedsaktørene vurderer avveininger på lang sikt. Dette gjelder imidlertid bare for perioder der det faktisk handles verdipapirer av et visst volum. Utviklingen etter finanskrisen i 2008 og særlig etter Eurokrisen det siste året har illustrert hvor uklart det er hva som kan anses som en risikofri rente og hva som er risikotillegget. I dagens marked er generelt alle yield-kurver stigende, dvs. at renten blir høyere med lengre løpetider for de tidsrom der det finnes likvide markeder.
Dagens rentenivå i markedet for antatt sikre papirer er generelt meget lavt i historisk sammenheng. Det er usikkert om dette kan sees på som en langvarig tendens, eller må sees på som et spesifikt forhold, gitt de mer spesielle forhold i dagens internasjonale valutamarked med betydelig risiko knyttet til bankenes generelle evne til å klare seg uten statlig støtte i Europa og USA kombinert med svak tillit til visse staters evne til å håndtere sine eksplisitte og implisitte forpliktelser.
For den norske staten har vurderinger av avkastning på de internasjonale finansmarkedene langt fram i tid en særskilt stilling, siden avkastningen på Statens pensjonsfond – utland kommer fra disse markedene. Meld. St. 17 (2011-2012) drøfter derfor både historisk og framtidig avkastning på svært lang sikt inngående. Det vises at den gjennomsnittlige årlige realavkastning på Statens pensjonsfond – utland på 2,7 prosent ligger godt innenfor normale svingninger rundt en forventning på 4 prosent.10 Det pekes på at dagens realrenter er svært lave, også sett i historisk sammenheng. Det skyldes ifølge stortingsmeldingen dels den kraftige nedgangsperioden verdensøkonomien har vært gjennom siden 2007, og dels sentralbankenes ønske om å stimulere til økonomisk vekst. Det ekstraordinære ved dagens situasjon taler etter Finansdepartementets syn for at en bør være varsom med å endre anslagene for forventet realavkastning av Statens pensjonsfond – utland utelukkende på grunnlag av dagens lave realrentenivåer. Forventet realavkastning på fondet er basert på et anslag for gjennomsnittlig avkastning på fondets portefølje av statsobligasjoner på 2,5 prosent og et anslag på aksjepremien på 2,5 prosent. Øvrige investeringsobjekter antas å ha en risikoprofil som ligger mellom statsobligasjoner og aksjer.
Avkastningskrav for offentlige prosjekter bør fastsettes som aritmetiske gjennomsnitt11 før skatt. Forventet langsiktig avkastning på aksjer i Statens pensjonsfond – utland er beregnet målt etter bedriftsskatt og uttrykker et geometrisk gjennomsnitt. Dette må derfor justeres for å kunne sammenlignes med avkastningskrav for offentlige prosjekter. Dersom man benytter den forventede avkastningen på porteføljen av statsobligasjoner på 2,5 prosent som den risikofrie referanseavkastningen, finner en ved hjelp av regneeksempelet i NOU 2009: 16, boks 8.2 et reelt risikotillegg (før skatt) for et gjennomsnittsprosjekt finansiert i aksjemarkedet på 3,5 prosent, gitt de forutsetninger som er gjort i boks 8.2 i NOU 2009: 16.12 Alternativt kunne vi sett bort fra en anslått løpetidspremie i porteføljen av statsobligasjoner og således tatt utgangspunkt i 2 prosent som en risikofri referanserente og fått 4 prosent som det relevante risikotillegget. Begge disse tilnærmingene tilsier at et reelt avkastningskrav på 6 prosent til prosjekter med om lag samme systematiske risiko som et gjennomsnittsprosjekt finansiert på det globale aksjemarkedet er konsistent med forventningene til den langsiktige avkastningen av aksjeporteføljen i Statens pensjonsfond – utland.
Hvis vi antar at et normalt offentlig tiltak, som et samferdselstiltak, har en risikoprofil som ligger noe nærmere en statsobligasjon enn et gjennomsnittlig prosjekt finansiert på børsen, tilsier beregningene ovenfor at et risikojustert reelt avkastningskrav (før skatt) på om lag 4 prosent er rimelig. Dette tilsier et risikotillegg på 1,5 prosentpoeng. En anvendelse av gjeldende tilrådninger om direkte beregning av risikotillegg, slik disse framgår i Finansdepartementets veileder fra 2005, har vist seg å gi lavere risikojustert rente enn det en slik rimelighetssjekk skulle tilsi.13
5.6 Samfunnsøkonomisk kalkulasjonsrente i andre land
Anbefalinger om kalkulasjonsrenter varierer sterkt mellom land. Én gjennomgang viser anbefalinger som spenner fra 1 til 15 prosent (Harrison, 2010). Nedenfor vil vi presentere noen utvalgte anbefalinger. Ulike land legger vekt på forskjellige hensyn i sin drøfting og fastsettelse av kalkulasjonsrente. Vi har valgt å gjengi anbefalingene slik de framgår av de dokumentene som er gjennomgått.
5.6.1 Anbefalinger for EU-området
Et konsortium ledet av det tyske instituttet IER (Universität Stuttgart, Institute of Energy Economics and the Rational Use of Energy) har i perioden 2004-2006 blant annet utarbeidet et forslag til harmoniserte retningslinjer for transportinfrastrukturinvesteringer i Europa gjennom et EU-finansiert forskningsprosjekt kalt HEATCO (Harmonised European Approaches for Transport Costing and Project Assessment). Det gis ikke én entydig anbefaling om kalkulasjonsrente for infrastrukturprosjekter. Det pekes snarere på at noen land tar utgangspunkt i ”samfunnets tidspreferanserate” som uttrykt gjennom Ramsey-betingelsen mens andre tar utgangspunkt i anslag på kapitalens alternativavkastning. For analyser av transportinfrastrukturinvesteringer på tvers av landegrenser anbefales det å benytte en risikofri rente eller et vektet gjennomsnitt av avkastningskravene i de ulike landene, vektet med finansieringsbidraget til det enkelte land. Det framgår ikke hvordan den risikofrie renten skal utregnes. Det anbefales sensitivitetsanalyser der det benyttes en rente på 3 prosent som i retningslinjene er begrunnet ut fra Ramsey-betingelsen, med p=1,5, µ=1 og g=1,5. For prosjekter i land som selv anbefaler bruk av en fallende rentekurve på lang sikt, anbefales det sensitivitetsanalyse med en fallende rentekurve for virkninger som inntreffer fra 40 år og utover.
Det gis ingen spesiell vurdering av om man skal korrigere kostnader eller kalkulasjonsrente for risikoaversjon. Risiko og usikkerhet anbefales derimot synliggjort gjennom sensitivitetsanalyser, scenarioanalyser og/eller Monte-Carlo simuleringer, alt etter som hvor store ressurser som er tilgjengelig og datagrunnlaget man har. Det gis ingen spesiell omtale av behandling av systematisk og usystematisk risiko.
5.6.2 Sverige
Det foreligger ikke sektorovergripende nasjonale føringer for valg av kalkulasjonsrente i Sverige. Innen samferdselssektoren anbefaler et utvalg nedsatt av det svenske Trafikverket at det tas utgangspunkt i HEATCO og anbefalingene i Storbritannia (Trafikverket 2012) ved fastsettelsen av kalkulasjonsrenten. Det tas utgangspunkt i Ramsey-modellen (se omtale over). Den rene tidspreferanseraten og grensenytteelastisiteten settes til det samme som ligger til grunn i Storbritannia (HM Treasury 2003) og som pekes på i HEATCO-retningslinjene. Økonomisk vekst i Sverige anslås til 1,78 prosent årlig. Samlet tilsier det en kalkulasjonsrente på 3,28 prosent. Det vises til argumenter for en fallende rente over tid, men det pekes på at de metodiske verktøyene som benyttes i samfunnsøkonomiske analyser av samferdselstiltak i Sverige ikke er tilpasset en slik fallende kurve. En noe lavere kalkulasjonsrente enn den på 4 prosent som var anbefalt tidligere antas å oppveie delvis for dette. Kalkulasjonsrenten var på 4 prosent fram til september 2012, men de nye retningslinjene som gjelder fra september 2012 tilrår 3,5 prosent.
5.6.3 Danmark
Det danske finansministeriet (Finansministeriet 1999) legger til grunn at den samfunnsmessige avkastning på kapital i alternativ anvendelse skjønnsmessig vil ligge i intervallet 6-11 prosent. 6 prosent velges som kalkulasjonsrente for å ta høyde for at offentlige investeringer antakelig har en lavere systematisk risiko enn et gjennomsnittlig prosjekt på børsen. Det påpekes i de danske retningslinjene at det valgte nivået vurderes også å ligge innenfor det sannsynlige intervall for samfunnets tidspreferanserate.
5.6.4 Storbritannia
I Storbritannia er kalkulasjonsrenten basert på samfunnets tidspreferanserate og tallfestet til 3,5 prosent reelt (HM Treasury 2003). Den britiske veilederen i samfunnsøkonomiske analyser, ”the Green Book”, ble revidert i 2003. Den tidligere kalkulasjonsrenten på 6 prosent inneholdt et risikopåslag for ulike risikoelementer. I revisjonen kom en imidlertid til at det var en bedre løsning å håndtere relevante risiko spesifikt i det enkelte prosjekt gjennom ulike metoder for risikohåndtering. Videre har britene utarbeidet egne retningslinjer for hvordan myndighetene ved beregning av de forventede nytte- og kostnadsstrømmene kan korrigere for en tendens til å være for optimistisk i prosjektvurderingene, såkalt ”optimism bias”, og således ta sikte på å få mer forventningsrette anslag. I ”the Green Book” legges det til grunn at systematisk risiko vanligvis er neglisjerbar for de fleste individuelle prosjekter gitt deres størrelse i forhold til nasjonalinntekten.14
På grunn av usikkerhet om fremtiden anbefaler den britiske veilederen en fallende kalkulasjonsrente over tid for prosjekter med virkninger utover 30 år. Det vises til Weitzman (1998, 2001) og et upublisert paper av Christian Gollier fra 2002. Retningslinjene inkluderer en tabell med hvilke diskonteringsrente som skal benyttes for virkninger i ulike tidsintervaller, med 3,5 prosent fram til år 30, deretter 3,0 prosent fram til år 75, og videre fallende til 1 prosent for virkninger som inntreffer i år 300 og utover. Det framgår ikke hvordan man har kommet fram til den konkrete rentekurven som anbefales.
5.7 Utvalgets vurdering
I samfunnsøkonomiske analyser er det nødvendig å sammenligne virkninger som inntreffer på ulike tidspunkt. En systematisk og transparent måte å gjøre dette på er ved diskontering med en kalkulasjonsrente, slik at alle prissatte virkninger omregnes til den verdien de vil ha i et gitt henføringsår kalkulert med en slik rente og derfor blir sammenlignbare. Når henføringsåret er i starten av tiltakets levetid, kalles dette for nåverdiberegninger.
Det er vanskelig å finne noen allmenngyldig fasit på hvilken kalkulasjonsrente som er ”riktig” eller hvordan en slik rente skal anslås. Det er imidlertid rimelig å ta utgangspunkt i at verdier i framtiden verdsettes noe lavere enn verdier i dag, sett fra dagens perspektiv.
En enkel tilnærming er å si at avkastningskravet avhenger av en ren tidspreferanserate, grensenytteelastisiteten som viser relativ endring i grensenytten dividert på relativ endring i konsum, og anslag på vekst i konsumet. Alle disse størrelsene er imidlertid på lang sikt svært usikre, og i kapittel 5.2.1 framgår det at ulike anslag på disse sentrale størrelsene har resultert i anslag på kalkulasjonsrente som spenner fra 1,4 til 8 prosent. Storbritannia og Sverige anbefaler renter på 3,5 prosent på kort sikt basert på et sett med forutsetninger som der antas rimelige.
Likeledes har vi avkastningskravet i finansmarkedet som gitt velfungerende markeder reflekterer avkastningen på private investeringer. Teoretisk er avkastningskravet for tilsvarende investeringer i utlandet alternativkostnaden for et offentlig tiltak og er således kalkulasjonsrenten for en liten åpen økonomi. I NOU 1997: 27 ble det pekt på at Norge er en liten, åpen økonomi, og i særdeleshet etter at kapitalmarkedet var blitt mer åpnet opp. Denne utviklingen har blitt forsterket siden 1997, noe som isolert sett tilsier at argumentene fra NOU 1997: 27 om å bruke en rentemodell basert på en alternativ vurdering av prisen på kapitalen ikke har svekket seg.
Reell risikojustert kalkulasjonsrente (før skatt) bør reflektere risikofri rente og risikoen i prosjektet og således reflektere prosjektets alternativkostnad. Ut fra en alternativkostnadstankegang vil det i utgangspunktet være fornuftig å justere kalkulasjonsrenten for det enkelte tiltak ut fra dets systematiske risiko. Den systematiske risikoen avhenger av om landet går bra eller dårlig når avkastningen fra prosjektet er ventet å komme. Hvis økonomien går godt, kan man forvente at prosjektets bidrag til landets verdiskaping er mindre verdsatt. Dette kan komme fram i analysen ved å bruke en høyere kalkulasjonsrente.
Det er imidlertid ikke opplagt hvordan et slikt prosjektspesifikt risikotillegg skal anslås. En riktig beregning av risikoen knyttet til enkelttiltak er komplisert i tillegg til at datagrunnlaget er dårlig. Erfaringen med slik prosjektspesifikk beregning av risikopåslaget har vist at slike beregninger i liten grad har blitt utført, og i de tilfellene det har blitt utført, er resultatet sårbart for endrede forutsetninger og mindre endringer i datagrunnlag. Som pekt på i kapittel 5.5 har direkte anvendelse av tilnærmingen i Finansdepartementets veileder fra 2005 også gitt lavere risikopåslag enn det en rimelighetssjekk skulle tilsi. I kapittel 5.2.4 redegjøres det for teorimessige svakheter ved å anvende kapitalverdimodellen for å anslå risikopåslaget for offentlige tiltak. I dette kapittelet er det vist til svakheter ved kapitalverdimodellen både når det gjelder å identifisere den systematiske risikoen i aksjemarkedet, og som utgangspunkt for å tilnærme seg det relevante risikopåslaget for et offentlig prosjekt. Utvalget mener derfor at denne modellen ikke er et godt grunnlag for å fastsette kalkulasjonsrenten for offentlige prosjekter.
Den faglige utviklingen, særlig i lys av klimadebatten, har gitt mye ny og interessant analyse av verdsetting av virkninger på særlig lang sikt. Som en oppsummering kan vi si at teorien som er gjennomgått tilsier at risikofri rente skal være fallende over tid dersom usikkerheten omkring vekstrater i økonomien akkumulerer over tid. Hvis usikkerheten ikke akkumulerer, kan det likevel argumenteres for fallende renter over tid ut fra forventet fallende vekstrater over tid. Hyperbolsk diskontering er en alternativ begrunnelse for fallende renter. Det foreligger imidlertid ingen tilsvarende konsensus om hvordan den konkrete tidsutviklingen på rentekurven er, og gjennomgangen i kapittel 5.4.1 viser at ulike antakelser gir ulik tidsprofil. Samtidig er det en pågående debatt om hvordan prosjektspesifikk systematisk risiko på lang sikt påvirker den samfunnsøkonomisk relevante risikopremien. Bidraget fra Weitzman (2012) peker på at man for prosjekter med systematisk risiko lavere enn markedsgjennomsnittet, vil få en rente som på lang sikt faller mot den risikofrie renten.
Litteraturen gjennomgått ovenfor peker samlet sett på at økende usikkerhet om alternativavkastningen tilsier fallende kalkulasjonsrente. Den økonomiske begrunnelsen for dette er at det blir mer attraktivt å realisere prosjektet ettersom usikkerheten rundt alternativavkastningen øker. Dette gir et lavere sikkerhetsekvivalent avkastningskrav som betyr en lavere kalkulasjonsrente. Litteraturgjennomgangen i dette kapittelet har vist at det er støtte for at usikkerheten om den makroøkonomiske utviklingen - og dermed alternativavkastningen - er stigende på særlig lang sikt, utover den perioden man med rimelighet kan sikre seg i finansmarkedene. Denne litteraturen tilsier således at kalkulasjonsrenten, vurdert fra analysetidspunktet, bør være fallende med tiden. Samlet sett mener utvalget at kalkulasjonsrenten til bruk i samfunnsøkonomiske analyser av offentlige tiltak bør reflektere disse argumentene for fallende diskonteringsrente som følger av teorien som er presentert i kapittelet, særlig for svært langsiktige prosjekter.
Når utvalget skal gi tilråding om diskonteringsrente til bruk i vurdering av offentlige tiltak, må vi også ta hensyn til beslutningsstrukturen dette inngår i. Et stort rom for skjønn hva gjelder anslag på prosjektspesifikk risiko, rentens tidsstruktur og prosjektets levetid vil kunne gi incentiver til å velge forutsetninger som kan påvirke resultatet av analysen i den retningen ulike aktører ser seg tjent med. I tillegg tyder erfaringene fra tidligere praksis med flere risikoklasser på at mange prosjektanalytikere har vært usikre på de faglige kriteriene for valg av risikoklasse, og at valget derfor tidvis kan synes å ha vært noe vilkårlig. Disse forholdene taler for å anbefale enkle og transparente regler som fanger opp de viktigste sidene ved problemstillingen, men som ikke blir for kompliserte å forstå eller å anvende. På den annen side vil enkle, men rigide regler nødvendigvis begrense analytikerens mulighet til å ta hensyn til mer spesifikk kunnskap om det enkelte prosjekt, for eksempel hva angår systematisk risiko.
Det finnes ikke én korrekt måte å gi konkrete anslag på risikofri rente, risikopåslag og tidsprofil for renteutviklingen. En rimelig tilnærming kan imidlertid være å anta at det under normale markedsforhold innenfor et tidsspenn på 40 år er mulig å sikre en risikofri realrente på 2,5 prosent ved plasseringer i det internasjonale finansmarkedet. Dette er på nivå med ubetinget forventet avkastning på statsobligasjoner i Statens pensjonsfond – utland. Utover 40 år er det rimelig å anta at man ikke kan sikre en langsiktig rente i markedet, og kalkulasjonsrenten bør settes ut fra en vurdering av sikkerhetsekvivalent rente. En risikofri diskonteringsrente på 2 prosent vil kunne være i tråd med rimelige forutsetninger om utviklingen av usikkerheten om framtidig økonomisk utvikling.
Videre må kalkulasjonsrenten reflektere at normale offentlige tiltak, som et samferdselstiltak, til en viss grad vil være følsomme for endringer i den generelle økonomiske situasjonen (systematisk risiko). Utvalget mener at kapitalverdimodellen ikke er et godt utgangspunkt for å fastslå hvilket risikotillegg som vil reflektere dette på en god måte. I tråd med prinsippet om at kalkulasjonsrenten skal reflektere alternativkostnaden, og som en enkel og transparent regel, mener utvalget at det er rimelig å se hen til forventet avkastning på Statens pensjonsfond – utland, som eier en liten andel av verdens produksjonskapasitet og gjeld. For fondets portefølje er det anslått forventet gjennomsnittlig avkastning på statsobligasjoner på 2,5 prosent og risikopremie for aksjer på 2,5 prosent. I kapittel 5.5 redegjøres det for at et avkastningskrav på et normalt offentlig tiltak, som et samferdselsprosjekt, på 4 prosent er konsistent med disse forventningene. Tabell 5.2 skisserer en struktur for diskonteringsrente for et slikt normalprosjekt på dette grunnlaget.
Utvalget anbefaler at strukturen skissert i tabell 5.2. normalt benyttes for diskontering av alle typer offentlige tiltak. Etter en samlet vurdering anbefaler en dermed ikke etablering av flere risikoklasser med ulike risikojusterte diskonteringsrater. For tiltak som helt klart har lav eller negativ systematisk risiko, som for eksempel arbeidsmarkedstiltak, vil det være naturlig å bruke en kalkulasjonsrente som er lavere. For tiltak som har helt klart høyere systematisk risiko vil det tilsvarende være riktig å bruke en kalkulasjonsrente som er høyere. Dersom man for øvrig ønsker å gjennomføre en følsomhetsanalyse av hvordan prosjektets netto nytte vil påvirkes av andre forutsetninger om systematisk risiko, vil det være naturlig å gjøre det som et tillegg, slik at man har en basisanalyse som sikrer sammenlignbarhet i beslutningsprosessen. For prosjekter hvor det primært er kostnadssiden som er kvantifisert, må vurderingene av konjunkturfølsomhet knyttes til kostnadssiden. For offentlig forretningsdrift i direkte konkurranse med private aktører vil det imidlertid være naturlig å benytte et risikotillegg som tilsvarende private bedrifter står overfor.
Tabell 5.2 Struktur for diskonteringsrente for et normalprosjekt
Diskonteringsrente | |||
0-40 år | 40-75 år | fra 75 år (dvs. i stor grad miljøvirkninger) | |
-risikofri rente | 2,5 prosent | 2 prosent | 2 prosent |
-påslag | 1,5 prosent | 1 prosent | 0 prosent |
Risikojustert rente | 4 prosent | 3 prosent | 2 prosent |
Det har tidligere ikke vært vanlig å anvende en rente som varierer over tid i samfunnsøkonomiske analyser. Det er derfor verdt å presisere to forhold. For det første er bakgrunnen for fallende rente, slik det er presentert ovenfor, økende usikkerhet over tid. I en utredningssituasjon der en slik fallende rente skal anvendes, vil det derfor være riktig å legge til grunn at rentestrukturen vil gjelde fra analysetidspunktet. For det andre skal verdier i samme periode diskonteres ned med samme diskonteringsrente. Sett at en fallende kalkulasjonsrente operasjonaliseres med én rente de første 40 år og en lavere rente for årene deretter. Da skal en virkning i år 50 først diskonteres ned til år 40 med den lave renten, og videre derfra med den mer kortsiktige renten. Det er med andre ord ikke snakk om at en virkning kan endre verdi vesentlig ved å flyttes fra år 40 til år 41, eller lignende.
I dag legges det til grunn en ambisjon om at prising av systematisk risiko skal håndteres individuelt for prosjekter som faller inn under den statlige ordningen for kvalitetssikring av konseptvalg (KS1). Med dagens retningslinjer gjelder dette prosjekter med forventet kostnad over 750 mill. kroner. Utvalget peker imidlertid på at det later til å være vanskeligere enn antatt tidligere lagt til grunn å identifisere risikopremien som på en korrekt måte reflekterer enkeltprosjekters systematiske risiko, og mer spesifikt at metoden som har vært anbefalt til nå, med utgangspunkt i kapitalverdimodellen, har svakheter. Dette taler isolert sett for at det ikke stilles krav om prosjektspesifikke risikopåslag. Utvalget mener videre at det vil være et mer forutsigbart system dersom kalkulasjonsrenten settes på samme måte for alle offentlige tiltak, uavhengig av om de faller innunder ordningen for ekstern kvalitetssikring av konseptvalg (KS1).
Utvalget peker avslutningsvis på viktigheten av at verdiene av virkningene som inngår i analysen er korrekte, før diskontering. Utvalgets anbefalinger i denne rapporten vil i stor grad bidra til at verdsettingen av verdiene av virkningene i analysen før diskontering blir mer korrekte, jf. kapittel 4 om realprisjustering og kapittel 9 om karbonprising. Der det er stor usikkerhet om virkningene av tiltaket, bør det både legges stor vekt på å sikre forventningsrette estimater og best mulig belysning av usikkerheten, gjerne gjennom egne følsomhetsanalyser av virkningene. Usikkerhetsanalysene som gjøres i utarbeidelsen av konseptvalgsutredninger og KS1 er verdifulle blant annet ved at de bidrar til å framskaffe mer forventningsrette estimater for nytte- og kostnadsvirkninger.
5.8 Oppsummerende tilrådinger
I prinsippet bør reell risikojustert kalkulasjonsrente reflektere risikofri rente og risikoen i prosjektet og således reflektere prosjektets alternativkostnad, men diskonteringsrenten til bruk i vurdering av offentlige tiltak bør imidlertid være basert på enkle regler som fanger opp de viktigste sidene ved problemstillingen.
For offentlig forretningsdrift i direkte konkurranse med private aktører vil det være naturlig å benytte en kalkulasjonsrente som tilsvarende den som private bedrifter står overfor.
Til bruk i samfunnsøkonomisk analyse av et normalt offentlig tiltak, som et samferdselstiltak, vil en reell risikojustert kalkulasjonsrente på 4 prosent være rimelig for virkninger de første 40 år fra analysetidspunktet.
Utover 40 år er det rimelig å anta at man ikke kan sikre en langsiktig rente i markedet og kalkulasjonsrenten bør da settes ut fra en fallende sikkerhetsekvivalent rente. For årene fra 40 til 75 år fram i tid anbefales en rente på 3 prosent. Som diskonteringsrente for årene deretter anbefales en rente på 2 prosent.
5.9 Litteraturliste
Atkinson, G., S. Dietz, J. Helgeson, C. Hepburn og Håkon Sælen (2009). Siblings, Not Triplets: Social Preferences for Risk, Inequality and Time in Discounting Climate Change. Economics e-journal, Vol. 3 (26).
Banz, R. (1981). The relationship between returns and market value of common stock. Journal of Financial Economics, 9, s. 3-18.
Campbell, J, Y. og L. M. Viceira (2003). A multivariate model of strategic assets allocation, Journal of Financial Economics 67, s. 41–80.
Cline, W.R. (1993). Give Greenhouse Abatements a Fair Chance, Finance and Developement (3): s. 3-5.
Cochrane, J. H. (2005). Asset Pricing: Revised Edition. Princeton, NJ: Princeton University Press.
Dasgupta, P. og E. Maskin (2005). Uncertainty and Hyperbolic Discounting, American Economic Review, 95(4), s. 1290-1299.
Dovre Group (2010). Veileder nr. X. Systematisk usikkerhet – omregning til risikojustert
rente.
Fama, E. F. og K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics, 33, s. 3-56.
Finansdepartementet (2005). Veileder i samfunnsøkonomiske analyser.
Finansdepartementet (2005b). Rundskriv R-109/2005.
Finansdepartementet (2011). Prop. 1 S (2011-2012) for Finansdepartementet.
Finansministeriet (1999). Vejledning i udarbejdelse af samfundsøkonomiske konsekvensvurderinger. Finansministeriet i Danmark.
Frederick, S., G. Loewenstein og T. O'Donoghue (2002). Time Discounting and Time Preference: A Critical Review, Journal of Economic Litterature, 40,s. 351-401.
Freeman, M. og B. Groom (2012) Positively Gamma Discounting! Mimeo. Submitted to the Economic Journal, April 2012.Gollier, C. (2002). Time horizon and the discount rate, Journal of Economic Theory, 107, s. 463-473.
Gollier, C. (2008). Discounting with fat-tailed economic growth, Journal of Risk and Uncertainty, 37, s. 171-186.
Gollier, C. (2011). On the under-estimation of the precautionary effect in discounting. CESifo working paper No. 3536 July 2011.
Harrison (2010). Valuing the Future: the social discount rate in cost-benefit analysis. Visiting Research Paper April 2010. Australian Government. Productivity Commission.
Harstad, B. (2012). Investment Policy for Time-Inconsistent Discounters. Upublisert notat, presentert på utvalgets konferanse om diskonteringsrente i Bergen 24-25. mai 2012. Tilgjengelig på http://www.sv.uio.no/econ/personer/vit/baardnh/dokumenter/discounting.pdf.
HEATCO (2006). Deliverable 5. Proposal for Harmonised Guidelines. Rapport, Developing Harmonised European Approaches for Transport Costing and Project Assessment.
Hepburn, C., Koundouri, P., Panopoulou, E. og Pantelidis, T. (2009). Social discounting under uncertainty: a cross country comparison. Journal of Environmental Economics and Management 57, s. 140-150.
HM Treasury (2003). Appraisal and Evaluation in Central Government (The Green Book), HMSO,London.
Jegadeesh, N. og S. Titman (1993) Returns to buying winners and selling losers: Implications for stock market efficiency. Journal of Finance, 48, s. 65-91.
Johnsen, T. (1996). Avkastningskrav ved vurdering av lønnsomheten I statlig eiet forretningsvirksomhet. SNF-rapport 90/96.
Laibson, D. (1997). Goldeneggs and hyperbolic discounting. Quarterly Journal of Economics, May 1997, s. 443-477.
Lintner, J. (1965). The Valuation of Risk Assets and the Selection of Risky Investments inStock Portfolios and Capital Budgets. Review of Economics and Statistics. 47:1, s. 13–37.
Meld. St. 17 (2011-2012) Forvaltningen av Statens pensjonsfond i 2011.
Merton, R.C. (1969), Lifetime portfolio selection under uncertainty: The continuous- time case, Review of Economics and Statistics (51), s. 247-257.
Minken, H. (2005): Nyttekostnadsanalyse i samferdselssektoren: Risikotillegget i kalkulasjonsrenta. TØI-rapport 796/2005.
Mossin, J. (1966). Equilibrium in a capital asset market. Econometrica 34: s. 768-783.
Mossin, J. (1968). Optimal multiperiod portfolio policies, Journal of Business, s. 215-229.
Newell, R. G. og W. A. Pizer (2003). Discounting the distant future: How much do uncertain rates increase valuations? Journal of Environmental Economics and Management. (46) s. 52-71.
Nordhaus, W. (2007a). The Stern Review on the Economics of Climate Change.
Nordhaus, W. (2007b). The Challenge of Global Warming. Economic Models and Environmental Policy.
NOU 1997: 27 Nytte-kostnadsanalyse.
NOU 2009: 16 Globale miljøutfordringer – norsk politikk.
Samuelson, P.A. (1969). Lifetime portfolio selection by dynamic stochastic programming, Review of Economics and Statistics (51), s. 239-246.
Sharpe, W, F. (1964). Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. Journal of Finance. 19:3, s. 425–442.
Stern, N. (2007). Stern Review on the Economics of Climate Change. HM Treasury, Storbritannia.
Trafikverket (2012). Samhällsekonomiska principer och kalkylvärden för transportsektorn: ASEK 5.
Vennemo, H (2011). Systematisk usikkerhet i praktiske samfunnsøkonomiske analyser. Vista Analyse AS Rapport 2011/25.
Weitzman, M. L. (1998). Why the Far-Distant Future Should Be Discounted at Its Lowest Possible Rate. Journal of Environmental Economics and Management, November 1998, 36(3), s. 201-08.
Weitzman, M. L. (2001). Gamma Discounting, American Economic Review (91:1)
Weitzman, M. L. (2012). On the Risk-Adjusted Discount Rate for Long-Term Public Investments. Unpublished. Tilgjengelig på http://nyttekost-web.sharepoint.com/Pages/default.aspx.
Fotnoter
Med avtakende grensenytte er grensenytteelastisiteten negativ, mens det er tallverdien av denne elastisiteten som opptrer i Ramsey-formelen.
Denne elastisiteten drøftes også i kapittel 3 om fordeling innenfor en og samme generasjon
I kapittel 3 pekes det på at det ikke er mulig å finne en metode for å estimere den ”riktige” grensenytten av konsum ut fra økonomisk teori alene, siden nyklassisk økonomisk teori anvender et nyttebegrep som ikke uten videre er målbart.
Se boks. 8.1 i NOU 1997: 27 for en formell gjennomgang av en slik stilisert modell.
Gjennomgangen av den generelle prismodellen og kapitalverdimodellen er i hovedsak basert på Cochrane (2005).
Optimeringsproblemet kan løses for ulike ”sett” av konkave nyttefunksjoner og avkastningsfordelinger. Dersom nytten er kvadratisk trengs det ingen antagelser om fordelingsegenskaper fordi en investor med slike risikopreferanser uansett bare vil være opptatt av forventning og varians. Det er denne nyttefunksjonen som er brukt i den klassiske utledningen av CAPM. Problemet med kvadratisk nytte er at den såkalt absolutte risikoaversjonen øker med økende formue, noe som er lite realistisk.
De øvrige forutsetningene er at investorer har konstant relativ risikoaversjon og at de bare lever av kapitalinntekter. De siste hundre årene har vi sett en stor vekst i konsum per capita og formue som ikke har vært akkompagnert av en langsiktig trend i renter og risikopremier. Det tyder på at investorers risikoaversjon ikke er spesielt avhengig av formue. Campbell og Viceira (2003) hevder på bakgrunn av dette at man som hovedregel kan og bør anta at investorer har konstant relativ risikoaversjon. Introduksjon av arbeidsinntekter vil i følge Campbell og Viceira (2003) under normale omstendigheter øke den optimale andelen plassert i aksjer.
Når det gjelder diskonteringsrentens tidsstruktur, viser Gollier (2008) at dersom preferansene utviser konstant relativ risikoaversjon, og konsumutviklingen følger en diskret stokastisk prosess der konsumendringene er stokastisk uavhengige og identisk fordelte, vil tidsstrukturen av renten være flat i den forstand at diskonteringsrenten vil være uavhengig av tidshorisonten. Hvis derimot konsumveksten er positivt korrelert over tid, vil konsumusikkerheten sett fra investeringstidspunktet forstørres jo lengre ut i tid konsumet skjer. Dette vil implisere en diskonteringsrente som faller med tidshorisonten. Dersom den stokastiske prosessen som ligger bak konsumutviklingen er gjenstand for såkalt «mean reversion» slik at konsumet kommer tilbake til et normalnivå som følge av konjunkturene, vil fallet over tid i diskonteringsrenten være betydelig mindre markert.
Se fotnote 8.
Det framgår av stortingsmeldingen at dette gjelder avkastningstall beregnet som geometriske gjennomsnitt (vekstrater).
Det aritmetiske gjennomsnittet, RA, av verdiene a1,a2 og a3 er ⅓(a1 + a2+a3). Det geometriske gjennomsnittet, RG, av de samme verdiene er
.
Dersom verdiene a1,a2 og a3 ikke er identiske, vil det geometriske gjennomsnittet være mindre enn det aritmetiske. Dersom suksessive avkastningstall er statistisk uavhengig og identisk fordelt med en varians lik σ 2, har vi at RG ≈ RA – 0,5σ2. Se for eksempel Johnsen (1996) for en nærmere drøfting.
Det er lagt til grunn en volatilitet knyttet til realavkastningen av aksjeinvesteringer på 15 prosent og en normalfordelt avkastning (lognormale aksjepriser). Videre er det lagt til grunn en gjennomsnittlig bedriftsskattesats ute på 25 prosent og en egenkapitalgrad på 50 prosent samt en lånerente for bedrifter på 5 prosent.
Se for eksempel Dovre Group (2010).
Det presenteres ikke noen nærmere begrunnelse eller kildehenvisning for dette i HM Treasury (2003).