6 Lifespan, analysis period and residual value
6.1 Introduction
From the terms of reference of the Committee:
The guide published by the Ministry of Finance does not prescribe the analysis period for a measure. The discrepancy between the analysis period and the technical lifespan is in certain sectoral guides dealt with by calculating a residual value as per the end of the analysis period. The Committee shall assess how the analysis period and the residual value should be determined.
A cost-benefit analysis should seek to capture all relevant effects of the measure under consideration. This suggests that if the measure will have effects into the distant future, such effects should also be captured. Cost-benefit analysis tends to focus on the net present value of the effects, such as to ensure the comparability of effects arising at different points in time. A discount rate is used to calculate the net present value, cf. the discussion in Chapter 5. This implies that effects in the distant future are accorded a low net present value, thus being, in relative terms, of minor importance to the overall assessment. At the same time, the uncertainty associated with the effects increases the further into the future these are expected to occur. If the measure under analysis has uncertain effects in the distant future, it may be appropriate to estimate any effects arising after a certain year on a rule-of-thumb basis. Chapter 5 on the discount rate also discusses the evaluation of measures with a particularly long time horizon.
In line with established terminology within the literature on cost-benefit analysis, as a specific method of analysis, we will define the analysis period as the period for which the effects of a project are analysed in detail. If the lifespan is expected to be longer than the analysis period, we may use the term residual value period to designate the remaining time period. The residual value is defined as the economic net present value a project is expected to generate after the expiry of the analysis period, estimated on a rule-of-thumb basis. The sum of the net present value from the analysis period and the residual value should provide the best possible estimate for the overall effects of the measure throughout its entire lifespan. Chart 6.1 illustrates the relationship between the project lifespan, the analysis period and the residual value period.

Figure 6.1 Illustration of lifespan, analysis period and residual value period1
1 A cost-benefit analysis should capture effects throughout the entire lifespan of the project. If the lifespan is T years, and precise cost and benefit estimates are only prepared for n years (the analysis period), one should calculate a residual value that captures the estimated net present value for the remaining part of the project’s lifespan (the residual value period). Hence, the net present value of the sum of the costs and benefits from the analysis period and the residual value represents the estimated net benefits of the project
In the present Chapter, the Committee will start out by discussing the lifespan of a project in Chapter 6.2 and principles for determining the analysis period in Chapter 6.3. Thereafter, we will, in Chapter 9.4, address various methods for estimating a residual value. In Chapter 6.5, we then present the methods recommended in sectoral guides in Norway and in foreign guides. Finally, the assessment of the Committee is presented in Chapter 6.6 and its recommendations in Chapter 6.7.
6.2 Lifespan
The lifespan of a measure may be defined as the period during which the measure under analysis will actually be in use or of service to society. The lifespan of a measure will depend on the specific nature of the project and the sector in question. This may be estimated using different approaches.
One approach is to start out from such lifespan as results in the maximum positive net present value. This may be termed the optimal lifespan of the measure.1 If one examines an investment involving operational and maintenance costs that increase over time, whilst the benefits do not increase correspondingly, one may find a point where annual costs exceed the annual benefit flow from the project. If the project is economically profitable with such lifespan, this will define the optimal lifespan of the project. However, use of an optimal lifespan in the analysis is conditional upon it being reasonable to expect that the operating period of the facility will in actual fact be determined on the said basis. Such is not always the case with public sector projects. Any significant non-priced effects from the project should also be taken into consideration in evaluating what is the optimal lifespan of the project. The same applies to any significant costs associated with closing down the project at the end of its lifespan. In an international context, such is for example the case when analysing a nuclear power plant. Although the concept of optimal lifespan has its limitations, it may offer a basis for assessing what is an appropriate lifespan for projects within the relevant sector.
A related term is the technical or physical lifespan of an investment. This will be the lifespan of physical elements of the investment until they can no longer be used and will need to be replaced in their entirety. Although this term may seem objective, elements of discretionary assessment will be involved here as well. Operational and maintenance costs must always be expected during an operating phase, and there will not always be a clear distinction between what constitutes maintenance and what should be classified as reinvestment. How high operational and maintenance costs one believes to be reasonable to keep an investment in use will also be a matter of discretionary assessment. For many facilities, different components will have different lifespans, thus in any case requiring reinvestment in such components within the period defined as the overall technical or physical lifespan of the facility.
Some public sector measures do not comprise physical investments, but services and regulations. For such measures it is appropriate to consider how far into the future one expects the measure to have major effects.
If comparing projects with different lifespans that are intended to realise the same social objective, it will not be correct to compare their net present values directly, unless none of the projects can be implemented again in future. One approach is to show the costs and benefits of the various projects within the same time horizon. If one then chooses the project with the longest lifespan as the point of reference, reinvestments need to be taken into consideration for projects with shorter lifespans. In order to make the analysis sufficiently detailed, it is appropriate to include any operational, maintenance and reinvestments costs required to keep the functionality of the measure at a defined and adequate level within the time horizon of the analysis. Another approach, which should in theory give the same answer, is to focus on the annuity of each project, given its expected lifespan and the discount rate used. Such annuity is the fixed annual cash flow that has the same net present value as the project over the project lifespan. Annuities are comparable between projects with different lifespans. If one wishes to rank the projects based on their priced effects, one will rank the projects based on their annuities.
The lifespan of a given investment may often be subject to considerable uncertainty, as the result of uncertainty with regard to developments in demand, trends, technology, etc. This applies, inter alia, to ICT projects, for which it is difficult to know with any certainty when the solution becomes outdated and reinvestment becomes necessary. Where this can be expected to be a key issue, one may for example highlight it by making use of sensitivity and scenario analyses.
6.3 Analysis period
The analysis period is the period for which annual costs and benefits are estimated in detail in the cost-benefit analysis. In order to capture all relevant costs and benefits, the analysis period should as a main rule be identical to the lifespan of the measure.
However, there are some reasons why the analysis period may be shorter than the lifespan of the measure:
Mounting uncertainty about the magnitude of the effects in the long run, and thus also about the lifespan itself, may suggest that one might want to highlight for what time period one has a reasonably good basis for the precise modelling of effects, and for what time period this would not be particularly meaningful.
Estimates for key input data may not be available for the entire lifespan of the project (e.g. GDP growth, population growth).
The resources that would have to be devoted to preparing precise estimates for the distant future are disproportionate to the contribution such estimates would make to the cost-benefit analysis as a basis for making decisions.
If the analysis period is shorter than the lifespan of the measure, the calculation must be supplemented by the economic net present value one expects from the project after the expiry of the analysis period, estimated on a rule-of-thumb basis. Such an economic net present value estimated on a rule-of-thumb basis is defined as the residual value of the project. It is noted in the NOU 1997: 27 Green Paper that such an approach may be justified on two grounds:
Firstly, one may assume that the effects will from a certain point in time have become stable and remain at the same level in all eternity. In such case it will be simple to arrive at an expression for the residual value of the project and include it on the income side. An alternative reasoning may be that it is conceivable, if the purpose of the analysis is to rank mutually exclusive alternatives, that such ranking based on net present values will not be affected by what happens after a certain point in time. The reason for this can be that effects in the distant future may «disappear» through the discounting. It will in such case be adequate to choose an analysis horizon that ends at that point in time.
If one defines an analysis period that is shorter than the project lifespan, and estimates a residual value, the economic net present value of the project can be expressed as follows:
where NPV is the net present value, Bt is economic income in year t, Ct is economic cost in year t (including any cyclical reinvestment and upgrading costs), k is the discount rate, n is the number of years in the analysis period and is the residual value measured in year (n+1). Various methods estimating such a residual value are discussed in Chapter 6.4.
6.4 Residual value
The residual value is defined as the economic net present value one expects the project to generate after the expiry of the analysis period, as estimated on a rule-of-thumb basis. In the private sector one can expect a correlation between the market value of invested capital at a given point in time and the income flow one can expect from said capital after such point in time. There is not necessarily any such correlation for public sector projects. Consequently, it is necessary to perform an explicit assessment as to how the residual value can reflect expected future net benefits in the best possible manner.
The following requirements may be stipulated with regard to the calculation of a residual value:
The residual value should be capable of being calculated on the basis of readily available information, for example information available from the calculations pertaining to the analysis period.
The assumptions underpinning the calculation of the residual value should be readily comprehensible.
The residual value should provide the best possible estimate, based on available information, for the total economic net present value expected from the project from the expiry of the analysis period and until the project lifespan has come to an end.
Below, we will discuss alternative approaches for estimating a residual value for a project. The approaches are based on methods that are recommended either in Norway or in other countries.
Market value of capital equipment
As far as concerns used capital equipment for which a market exists, it will be appropriate to use an estimate for the sales price as per the end of the analysis period. In some cases, various circumstances may indicate that the investment is not saleable in practice, i.e. that its real market value is zero. Using market value is a simple method that meets the first two of the above criteria. However, the method will only meet the third criterion if a clear alternative use for the equipment/investment exists as per the end of the analysis period, and there is no significant market failure in the market in which the equipment can be sold. For most types of transportation infrastructure, for example a road, it is obviously difficult to envisage any secondary market, but for much of the materiel acquired by the armed forces, e.g. any weasels that have been procured, it may be more realistic to calculate the residual value on the basis of the market value.2
Straight-line depreciation
As far as concern investments for which it is difficult to envisage a secondary market or an alternative use, one will often use an alternative method based on the investment cost. Assume that the project lifespan is estimated to be 40 years, and that the analysis period is put at 25 years. The analyst will then need to estimate the remaining economic net present value; the residual value, of the project for the last 15 years of the project lifespan.
If one assumes that there is a correlation between the project cost and the economic value of the project, one may use an estimate for the residual value of the physical investment as an approximation for the residual economic value of the project. If one assumes that the value of the investment declines on a straight-line basis throughout the entire lifespan of the project, 15/40 of the investment value will remain after year 25. Such value may then be used as the residual value of the project for purposes of the analysis.
This method meets the first two criteria outlined above. The extent of the correlation between project cost and net economic benefit may, however, vary from project to project. There may often be little or no correlation at all. If, on the other hand, such correlation can be assumed to exist, the third criterion will also be met. If one has no reason to believe that such a correlation exists, the method will offer a poor estimate for the actual residual value of the project.
Residual value based on the net benefit flow in the last year of the analysis period
Another method may be to start out from the flow of net benefits generated by the project towards the end of the analysis period. The residual value may then be estimated on the basis thereof.
There may, as noted in the NOU 1997: 27 Green Paper, be cases in which one assumes that the effects of a measure will become stable towards the end of the analysis period, and remain at the same level for all eternity. In such case it will be simple to arrive at an expression for the residual value.
However, the lifespan is defined on the basis of for what length of time the measure under analysis will actually be in use or of service to society. This suggests, if one disregards non-valued elements, that the net benefit will have been reduced to zero in the last year of the lifespan. In such case the residual value may be based on the assumption that the annual flow of net benefits during the residual value period is gradually reduced to zero towards the end of the lifespan. One approach can be to assume that the flow of net benefits declines on a straight-line basis, in which case the residual value A will be defined by
where NB* is net benefits in the last year of the analysis period, n is the analysis period and T is the lifespan. This is illustrated in Chart 6.2.3
This method also meets the first two criteria outlined above. Whether it meets criterion number three depends on whether there is reason to believe that the flow of net benefits in the years from the end of the analysis period until the end of the project lifespan is determined by the flow of net benefits in the last year of the analysis period and then gradually reduced to zero towards the end of the lifespan.
One reason why the flow of net benefits in the years from the end of the analysis period until the end of the project lifespan may only to a limited extent be determined by the flow of net benefits in the last year of the analysis period could be cyclical changes in the net benefits from the project, for example due to reinvestment costs that recur at intervals of several years. This may be dealt with by adjusting the residual value for any cyclical or other expected variations in the time interval from the end of the analysis period until the end of the project lifespan, caused by for example major upgrading or reinvestment needs.
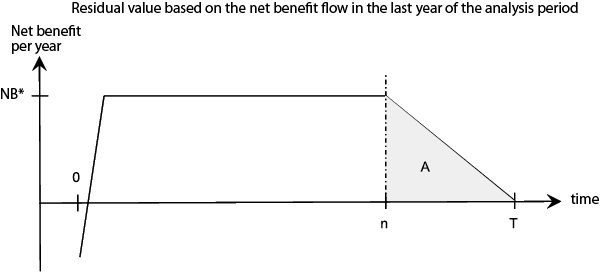
Figure 6.2 Residual value based on the net benefit flow in the last year of the analysis period
Scenario analysis
If the analyst believes that well-founded estimates are available for developments in key variables in the years from the end of the analysis period until the end of the project lifespan, one may envisage a model in which cost and benefit flows are extrapolated until the end of the project lifespan, as adjusted for different estimates for the said variables. One may, for example, operate with three scenarios, representing a low, a medium and a high alternative. The net present value of the net benefit flow, calculated for the years from the end of the analysis period until the end of the project lifespan in each scenario, will then represent the residual value of the project for use in the calculation of total estimated net benefits for the relevant scenario. The variation in net benefits between the various scenarios will in such case also illustrate how dependent the net benefits from the project are on developments towards the end of the project lifespan. The ambition should be for the mid scenario to reflect the expected value.
It may be more difficult to perform a scenario analysis in such a way that it meets the first two criteria for a residual value outlined at the beginning of this Chapter. It will be necessary to estimate developments in the key variables over the years after the end of the analysis period. This may require further analyses to supplement those carried out for the analysis period. It may furthermore, in view of mounting uncertainty associated with effects in the distant future, be more difficult to establish clear and unambiguous assumptions on which such estimates can be based. It may, on the other hand, be argued that the information about the net economic benefit from the residual value period, as estimated through a scenario analysis, is more suited for shedding light on the total economic net present value one expects the project to generate from the expiry of the analysis period and until the end of the project lifespan. This will imply improved compliance with the third residual value criterion. Since the approach will not provide one estimate, but several different estimates, for net economic benefits for the entire lifespan of the project, this approach may result in a more complex and equivocal basis for making decisions. It should be supplemented by assessments of the probabilities assigned to the various scenarios. This approach may be of particular relevance in cases where the residual value period is long and the uncertainty is high.
6.5 Current recommendations on analysis period and residual value
At present, the Ministry of Finance guide does not, as noted in the terms of reference, specify the analysis period for a measure. The NOU 1997: 27 Green Paper provides a brief discussion of the issue, as recapitulated in Chapter 6.3 above, but makes no specific recommendations either. Consequently, each sector in Norway has been left to choose its own approach to this issue. A review of recommendations in various sectoral guides in Norway and cost-benefit analysis recommendations in other countries identifies a broad range of approaches to the issues of lifespan, analysis period and residual value, cf. Tables 6.1 and 6.2 below. The tables will not necessarily convey all nuances of the various recommendations, and readers are referred to the sources for additional details.
The Swedish Transport Administration discusses analysis periods and residual values in a draft new cost-benefit analysis guide circulated for consultation (Swedish Transport Administration, 2012). The issues raised in the said draft are to a large extent the same as are addressed by the present Committee, and we will therefore add a brief summary to the observations made in the table below. It follows from Swedish Transport Administration (2012) that Sweden introduced a 40-year analysis period for investments within the transportation sectors with effect from the previous revision of its guide in 2008, whilst prior to that no specific analysis period had been stipulated. The reasons given at the time were the uncertainty associated with estimates for the very distant future, and that this is in line with practice in other countries and the recommendations emanating from the EU project HEATCO. It was recommended that any effects beyond this 40-year period be captured through a residual value. The method recommended for the calculation of residual value in the guide from 2008 was straight-line depreciation, as presented in Chapter 6.4 above. Swedish Transport Administration (2012) maintains the recommendation for a 40-year analysis period, but recommends, for projects with a lifespan in excess of 40 years, that the residual value of net benefits until the end of the project lifespan be estimated on the basis of the net benefit flow from the project in year 40. Swedish Transport Administration (2012) also presents recommendations with regard to economic life for different types of measures and elements, with a maximum economic life of 60 years.
Table 6.1 Recommendations on lifespan, analysis period and residual value in Norwegian sectoral guides
Norwegian sectoral guides | Lifespan | Analysis period1 | Residual value |
|---|---|---|---|
Norwegian Public Roads Administration (2006) | Refers to functional lifespan. Lifespan fixed at 40 years, unless otherwise indicated by special circumstances. | 25 years. | Straight-line depreciation. |
Norwegian National Rail Administration (2011) | Technical lifespan of the facility, or how long the service affected by the measure can be expected to have a market. Technical lifespan for different types of investment specified in the guide. Varies between 30 and 75 years. | 25 years; express reasons required for shorter or longer analysis periods. | In principle, the net present value of expected cash flow after the analysis period. Straight-line depreciation is the approach used for the time being. |
Norwegian Water Resources and Energy Directorate (“NVE”) (2003) | Economic life is the period over which the facility is depreciated for accounting purposes. Physical lifespan is the period during which the facility is expected to perform a function. (Ex. ordinary physical lifespan: hydropower (60 years), gas power and wind power (40 years)). | Normally same as economic life. (Ex. normal analysis period: hydroelectric power (40 years), gas power (25 years) and wind power (20 years)). | Straight-line depreciation. |
Statnett (2007) | Discusses lifespan for different types of facility (ex. overhead power line, steel poles (70 years), overhead power line, wood poles (50 years) and control facility (15 year)). | Normally 25 years. | Ideally speaking, the residual value shall express the net present value of having the facility in operation after the expiry of the analysis period, inclusive of necessary reinvestments. Straight-line depreciation used in practice. |
Norwegian Armed Forces (2010) | Separate analysis. | Often shorter than lifespan. | Market value. |
1 The specified period length often refers to the operating period only. In such case, a construction phase must be added. If, for example, the construction phase is 5 years and a 25-year analysis period has been specified, effects from a period of 30 years will be included in the detailed cost and benefit estimates.
Table 6.2 Recommendations on lifespan, analysis period and residual value in guides from other countries
Guides from other countries | Lifespan | Analysis period | Residual value |
|---|---|---|---|
Sweden (Swedish Transport Administration, 2012) | Economic life. (Specific list for different types of measures. Maximum lifespan 60 years.) | 40 years. | Continuation of net benefit flow from the last year of the analysis period. |
Her Majesty’s Treasury (HM Treasury, 2003) | Refers to “useful lifetime of the assets encompassed by the options under consideration”. | Should be the same as the lifespan. May deviate if public-private partnership. | Market value. Shall reflect any remaining value upon the expiry of the project lifespan (alternative use, market value or scrap value). Should be tested for sensitivity. |
UK Department for Transport (2011) | Most projects: indefinite. Some: finite. | For projects with indefinite lifespan: 60 years. For projects with finite lifespan: appropriate analysis period up to 60 years. | Analysis of projects with indefinite lifespan and 60-year analysis period described, in practice, as the scenario analysis in Chapter 6.4, but with only a mid-alternative being used. Any additional residual value after 60 years not estimated, but may be included in the form of a sensitivity test. For projects with finite lifespan: use the HM Treasury method, cf. the above table row. |
EU, HEATCO (2006) | Expected technical lifespan. | Investment period + up to 40 years’ operation. If several projects are compared: joint analysis period to end 40 years after the opening of the last project. | Straight-line depreciation. Alternative depreciation may be used if relevant (for example convex function for rolling stock). |
Danish Ministry of Finance (1999) | Economically optimal lifespan. | Normally same as economic life or the number of periods for which the service is to be provided. Sufficient length to capture relevant differences between alternatives under assessment. | Market value. |
6.6 The assessment of the Committee
A cost-benefit analysis should seek to capture all relevant effects of the measure throughout its lifespan. However, developments in terms of effects, and thus also in terms of lifespan, may be uncertain. It should therefore be the ambition of the sectors that the lifespan used in the analyses reflects the period during which the measures under analysis will actually be in use or of service to society.
However, the further into the future an estimate seeks to reach, the more uncertainty will be associated therewith. There will in many cases be a point beyond which it is no longer meaningful to prepare detailed cost and benefit estimates for use in cost-benefit analysis. Cost and benefit flows should be estimated as precisely as possible until such point in time. This is termed the analysis period. If the expected lifespan of the project exceeds the analysis period, the analysis needs to be supplemented by a residual value that shall provide the best possible representation of the remaining net economic benefit, based on readily available information. If there is considerable uncertainty associated with the lifespan, including whether it does exceed the analysis period, the residual value may be included in the analysis by way of a sensitivity analysis.
The duration of the analysis period is a matter of discretionary assessment. A review of recommendations within the transportation sector in Europe, HEATCO (2006), notes that it has turned out to be very difficult to provide specific estimates more than 40 years into the future. The Swedish Transport Administration has recommended, subsequent to the publication of the HEATCO report, a 40-year analysis period for transportation projects, based on the same reasoning. The transportation sector in Norway has used models with a shorter analysis period than this; 25 years. It is noted by the transportation bodies, in their proposed National Transport Plan 2014-2023, that such practice has been continued for road projects, whilst an analysis period of 75 years has been used for railway projects, with reinvestment costs being included in the analysis (Avinor et al., 2012). The Committee is of the view that it seems reasonable to expand the analysis period of these models, such as to provide detailed cost and benefit estimates for as much as possible of the project lifespan. However, the Committee agrees with the assessment of HEATCO and the Swedish Transport Administration that estimates into the very distant future will be highly uncertain, as well as with their recommendation that one should not seek to engage in detailed analysis of costs and benefits beyond a certain period. 40 years does, for example, seem a more appropriate analysis period for road projects than the 25 years used thus far. For other projects, both lifespans and analysis periods may be considerably shorter, e.g. in the region of 5-15 years for many ICT projects.
The presentation in Table 6.1 shows that most sectors in Norway use straight-line depreciation of the investment cost as a method for calculation of the residual value. Cost-benefit analysis is conducted in a highly uncertain world, and there are good reasons for choosing a simple rule-of-thumb model for effects in the very distant future. The straight-line depreciation method currently used in several sectors is an example of this. The Committee notes, however, that if there is little correlation between economic profitability and the actual prioritisation of projects, there will not necessarily be any close correlation between project investment costs and the net economic benefit generated by such projects when completed. Straight-line depreciation of investment costs does not, for such reason, seem a good calculation method for residual value.
The Committee therefore recommends that transportation bodies and others that currently calculate residual value on the basis of straight-line depreciation change their practice to calculating residual value based on knowledge of the specific cost and benefit flows estimated for the analysis period. One is then left with a choice, in line with the categorisation in Chapter 6.4 above, between estimating residual value on the basis of benefit flows from the last year of the analysis period and a scenario analysis. The reason for adopting an analysis period that may be shorter than the project lifespan is increased uncertainty, lack of estimates for key variables and a trade-off between the resources devoted to, and the benefits from, additional analysis. Since a scenario analysis may require a fair amount of resources, it may be inappropriate to choose scenario analysis as the primary approach. The Committee will therefore recommend that residual value be primarily estimated on the basis of the net benefit flow towards the end of the analysis period. For projects where most effects are valued, it should be assumed that the flow of net benefits approaches zero in the last year of the lifespan. It will therefore be reasonable to use, unless there is specific knowledge to the opposite effect, a calculation based on a gradual decline in net benefits, towards zero, from the end of the analysis period until the end of the lifespan, for such projects, cf. Chart 6.2.
This residual value must be adjusted for known variations, if any, that must be expected during the time interval from the end of the analysis period until the end of the project lifespan. These variations may, for example, relate to cyclical needs for major upgrades or reinvestments, and in such cases it may be more appropriate to focus on the average net benefit flow in the last cyclical period than on the net benefit flow in one single year for purposes of estimating the residual value. The specific approach should be made operational in future cost-benefit analysis guides, with a view to ensuring that the residual value is reasonably simple to estimate. The analysis may be supplemented by a sensitivity and scenario analysis, using different estimates for trend developments in the key drivers behind the cost and benefit flows. If there exist knowledge and documentation, including market value estimates, suggesting that a different method for estimating the residual value of the specific measure in question would be better, the best possible method should be used.
6.7 Summary recommendations
A cost-benefit analysis should seek to include all relevant effects of the measure throughout its lifespan.
The lifespan used in the analyses must reflect the period during which the measures under analysis will actually be in use or be of service to society. The lifespan therefore needs to be discussed for each project, or in sectoral guidelines within sectors where a large number of similar projects are implemented. It is appropriate for the approach within each sector to be as uniform as possible to ensure comparability between projects.
The main principle should be to bring the analysis period as close to the lifespan as practicable. It would, for example, seem more appropriate to apply 40 years as the analysis period for road projects than the 25 years applied until now.
If the analysis period is shorter than the lifespan of the measures, it will be necessary to calculate a residual value that estimates the total economic net present value the project is expected to generate from the end of the analysis period until the end of the project lifespan.
Residual value should principally be calculated on the basis of the net benefit flow over the last years of the analysis period. It should be adjusted for any cyclical or other expected variations during the time interval from the end of the analysis period until the end of the project lifespan, for example due to a need for major upgrades or reinvestments. For projects where most effects have been valued, it should be assumed that the flow of net benefits will approach zero in the last year of the lifespan.
The best possible method should be used in the event of any knowledge and documentation, including any market value estimate, suggesting that a different method for calculating the residual value of the specific measure in question would be better.
If the residual value period is assumed to be long and the effects (and thus the lifespan) are subject to considerable uncertainty, sensitivity analysis and scenario analysis should be used as supplementary analysis methods to shed light on the importance of particularly uncertain estimates.
6.8 Bibliography
Avinor, Norwegian National Rail Administration, Norwegian Coastal Administration and Norwegian Public Roads Administration (2012). Proposed National Transport Plan 2014-2023. Appendix. Presentation of major projects on national roads and railways. Calculation of greenhouse gas emissions. (In Norwegian only. Norwegian title: Forslag til Nasjonal transportplan 2014-2023. Vedlegg. Omtaler av store prosjekter på riksveg og jernbaner. Beregning av klimagassutslipp.)
Danish Ministry of Finance (1999). Guidelines for the conduct of economic impact studies. (In Danish only. Danish title: Vejledning i udarbejdelse af samfundsøkonomiske konsekvensvurderinger.) Danish Ministry of Finance.
Department for Transport (United Kingdom) (2011). Cost Benefit Analysis. TAG Unit 3.5.4. Transport Analysis Guidance (TAG).
HEATCO (2006). Deliverable 5. Proposal for Harmonised Guidelines. Report, Developing Harmonised European Approaches for Transport Costing and Project Assessment.
Ministry of Defence (2010). Cost-benefit analysis guide for investment activities within the defence sector. (In Norwegian only. Norwegian title: Veileder i samfunnsøkonomiske analyser for investeringsvirksomhet i forsvarssektoren.) Ministry of Defence.
HM Treasury (2003). Appraisal and Evaluation in Central Government (The Green Book), HMSO, London.
Norwegian National Rail Administration (2011). Method handbook JD 205, Cost-benefit analysis for the railways, Version 3.0, July 2011. (In Norwegian only. Norwegian title: Metodehåndbok JD 205 Samfunnsøkonomiske analyser for jernbanen, Versjon 3.0 Juli 2011.) Norwegian National Rail Administration.
Norwegian Public Roads Administration (2006). Impact Assessments. (In Norwegian only. Norwegian title: Konsekvensanalyser.) Handbook 140. Norwegian Public Roads Administration.
Norwegian Water Resources and Energy Directorate (2003). Cost-benefit analysis of energy projects. (In Norwegian only. Norwegian title: Samfunnsøkonomisk analyse av energiprosjekter.)Handbook. Norwegian Water Resources and Energy Directorate (“NVE”).
Statnett (2007). Cost-benefit analysis handbook. (In Norwegian only. Norwegian title: Håndbok for samfunnsøkonomiske analyser.) Statnett.
Swedish Transport Administration (2012). Economic Principles and Estimates for the Transportation Sector: ASEK 5. Preliminary Version 2. (In Swedish only. Swedish title: Samhällsekonomiske principer och kalkylvärden för transportsektoren: ASEK 5. Preliminär Version 2.)
Footnotes
The discussion of optimal lifespan adheres to the approach in the Danish cost-benefit analysis guide; Danish Ministry of Finance (1999).
A cost-benefit analysis may also be expanded by estimating the “scrap value” as per the end of the project lifespan. Such scrap value is fundamentally different from economic residual value discussed above, and will only include such values or claims as might remain in the project when the project is no longer providing any service for society or is no longer in use. It will be appropriate to use the expected market value as per the end of the project lifespan to calculate such “scrap value”.
Assume a lifespan of T years, an analysis period of n years and annual net benefits that are negative during a start-up period, and thereafter remaining stable at a positive level NN* for the remainder of the analysis period. Since the lifespan is defined with reference to when the project is no longer in use or of service to society, the residual value can be calculated as the area A on a rule-of-thumb basis.