3 Indicators of welfare improvement and sustainability

November 18, 2004 Geir B. Asheim1

3.1 Introduction 1

During the last few decades there have been important contributions on how to use national accounting aggregates to measure welfare improvement and sustainability. In this economic literature there is consensus about the following:

• For national accounting aggregates to be useful, the accounting must be made ‘comprehensive’ . The national accounts are ‘comprehensive’ if all variable determinants of current productive capacity are included in the vector of capital stocks, and if all variable determinants of current well-being are included in the vector of consumption flows. E.g., one must ”green” national accounts by (i) including depletion and degradation of natural capital as negative components to the vector of investment goods, and (ii) adding flows of environmental amenities to the vector of consumption goods.

• The central indicator for welfare improvement and sustainability is the genuine savings indicator, measuring thevalue of net changes in the comprehensive vector of capital stocks . The welfare significance of this indicator was shown by Weitzman (1976) and figures prominently in many contributions, see e.g. the recent paper by Arrow et al. (2003a). The value of net changes in the comprehensive vector of capital stocks is sometimes described as ”wealth changes at constant capital prices”.

• If sustainability is defined as the feasibility of sustaining the current level of well-being indefinitely, then the genuine savings indicator is only an imperfect indicator of sustainability (see Asheim, 1994). Still, the genuine savings indicator appears to have become the established sustainability indicator. On the one hand, there are conditions under which the genuine savings indicator can serve as a one-sided sustainability test (see Pezzey, 2004). On the other hand, some authors (see e.g. Arrow et al., 2003a, and other papers by Dasgupta and Mäler) choose to identify the concept of ‘sustainability’ with welfare improvement, for which a non-negative genuine savings indicator is an exact indicator.

There is more discussion about the role of comprehensive national income and comprehensive national wealth in indicating welfare improvement and sustainability.

• In a joint paper with Martin Weitzman (Asheim and Weitzman, 2001) we show how a positive genuine savings indicator corresponds to increased real NNP when a consumption price index is used to deflate prices. Hence, real NNP growth is an alternative to the genuine savings indicator , under the assumption of comprehensive accounting.

• Following Heal and Kriström (2003), comprehensive national wealth can be defined as the present value of future comprehensive consumption. However, national wealth indicates welfare improvement only under restrictive assumptions, as I will return to.

3.2 PV of future changes in comprehensive consumption

I start this overview in by presenting an entity–namely, the present value of future changes in comprehensive consumption–which (a) has welfare significance, (b) is related to various definitions of ”sustainable development”, and (c) we can hope to measure. To present this entity, I must first introduce consumption, consumption prices, and dis­counting by means of an interest rate.

Let the instantaneous well-being of the society at time t depend on a vector of consumption flowsC ( t ) that includes also environmental amenities. Let U be a utility function that assigns utilityU ( C ) to any consumption vector. Here, C is comprehensive, containing all variable determinants of current instantaneous well-being. This implies that society’s instantaneous well-being is increased by moving from C" ¢ to C " if and only if U ( C" ¢) < U ( C "). In the real world, U ( C ( t )) = U ( C^m ( t ), t ), where C^m ( t ) contains all variable and measurable determinants of instantaneous well-being at time t , while time, t , is included to capture all variable but un­measurable determinants.

Assume that resource allocation is optimal, and denote by P( t ) the real consumption price vector at time t, where prices are deflated by a consumption price index. The components of P ( t ) may correspond to market prices or calculated accounting prices. Let R ( t ) be the real interest rate at time t . Denote by p ( t ) the consumption price vector at time t , expressed in present value prices:

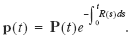
The present value of future changes in comprehensive consumption can then be defined as follows:

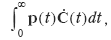
where denotes the vector of derivatives of C ( t ) with respect to time.

Assume that, at any time, society’s dynamic welfare is given by a Samuelson-Bergson welfare function defined over paths of utility from the present time to infinity, and that this welfare function is time-invariant. It then follows by a standard argument in welfare economics, as suggested by Samuelson (1961, p. 52) in the current setting, that dynamic welfare is increasing if and only if the present value of future changes in comprehensive consumption is positive. In particular, this conclusion holds in the case where society maximizes the sum of utilities discounted at a constant utility discount rate r, but not only in this case.

If one defines that the present behaves in a sustainble way if discounted utilitarian welfare is nondecreasing (see e.g. Arrow et al., 2003a, and other papers by Dasgupta and Mäler), it now follows that the present value of future changes in comprehensive consumption is an exact indicator of sustainability. If one the other hand, one defines that the present behaves in a sustainable way if it is feasible to sustain the present utility level indefinitely, then it follows from the analysis of Pezzey (2004) that one obtains a one-sided sustainability test, provided that society maximizes discounted utilitarian welfare: A non-negative present value of future changes in comprehensive consumption is necessary but not sufficient for sustainable development.

As stressed by Samuelson (1961), determining the sign of the present value of future changes in comprehensive consumption is not a comparison of wealth, but of ”wealth-like magnitudes”.

3.3 Measuring PV of future changes in comprehensive consumption

I then turn to a discussion of ways of measuring the present value of future changes in comprehensive consumption by comprehensive national accounting aggregates. Any direct attempt to estimate this entity would seem futile. In the words of (Samuelson, 1961, p. 53): ”We are left with the pessimistic conclusion that there is so much ’futurity’ in any welfare evaluation of any dynamic situation as to make it exceedingly difficult for the statistician to approximate to the proper wealth comparisons.” Fortunately, Weitzman (1976) and later contributions show that Samuelson was overly pessimistic. To present these developments, I have to describe the productive capacity of the society.

Let the productive capacity of the society at time t depend on a vector of capital stocksK ( t ) that includes not only the usual kinds of man-made capital stocks, but also stocks of natural resources, environmental assets, human capital (like education and knowledge capital accumulated from R&D-like activities), and other durable productive assets. Moreover, let I ( t ) (= , the vector of derivatives of K ( t ) with respect to time) stand for the corresponding vector of net investment flows . The net investment flow of a natural resource is negative if the extraction rate exceeds its natural growth.

Let ( C, I ) be attainable given K if and only if ( C, I ) is in S ( K ), where S ( K ) is a set that constitutes current productive capacity . Here, K is comprehensive, containing all variable determinants of current productive capacity. This implies that society’s productive capacity is changed by moving from K" to K" if and only if S ( K ") ≠ S ( K "). In the real world, S ( K ( t )) = S ( K^m ( t ), t ), where K^m ( t ) contains all variable and measurable determinants of productive capacity at time t , while time, t , is included to capture all variable but unmeasurable determinants.

Assume that resource allocation is optimal, and denote by Q ( t ) the real investment price vector at time t , where prices are deflated by a consumption price index. The components of Q ( t ) may correspond to market prices or calculated accounting prices. Denote by q ( t ) the investment price vector at time t , expressed in present value prices:

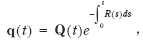
where R ( t ) still denotes the real interest rate at time t .

Then the value of net investments measures the present value of future changes in consumptions (see Weitzman, 1976, eq. (14), and Dixit et al., 1980, Theorem 1):

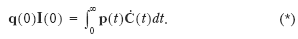
This motivates referring to the value of net investments, q (0) I (0), as the genuine savings indicator (coined by Hamilton, 1994) since it follows from (*) and the discussion of Section 2 that the value of net investments, q (0) I (0), is an indicator of welfare improvement and sustainability.

Moreover, if comprehensive real NNP , Y ( t ), is defined as the sum of the real value of consumption and the real value of net investments,

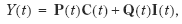
and Y( t) denotes the time derivative of Y ( t ), then, as shown by Asheim and Weitzman (2001),

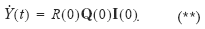
Hence, since Q (0) is proportional to q (0), it follows from (*), (**), and the discussion of Section 2 that growth in comprehensive real NNP is an alternative indicator of welfare improvement and sustainability, provided that the real interest rate, R (0), is positive.

3.4 The role of national wealth as an indicator

Samuelson (1961, p. 52) claims that ”there is no meaning in comparing money wealth in one situation (i.e. time and place) with that of another situation”, unless ”we use the same prices and interest rates in the comparison”. I now explore why this warning is pertinent.

If comprehensive real national wealth , W ( t ), is defined as the present value of future consumption,

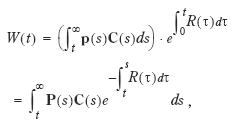
and ( t )denotes the time derivative of W ( t ), then

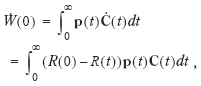
Hence, unless the real interest rate remains constant (i.e., for all t , R ( t ) = R (0)), then it follows from Section 2 that growth in comprehensive real wealth is not an indicator of welfare improvement and sustainability . The intuition is that capital gains arising from a changing interest rate should not be included in such an indicator. Moreover, national wealth need not equal the value of the current comprehensive capital vector (i.e.,

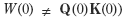
What assumptions are strong enough to ensure that changes in national wealth have welfare significance, and that national wealth is measured by the value of current comprehensive capital vector?

If society maximizes the sum of utilities discounted at a constant utility discount rate p , then the real interest rate R (t) is constant and equals p under the additional assumption that the utility function is linearly homogeneous; i.e., that a doubling of all consumption components leads to a doubling also of utility. This assumption can be interpreted as follows: A linearly homogeneous utility U does not include only variable and measurable consumption components C m, but also fixed or non-measurable components Cⁿ , so that utility at time t equals

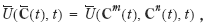
where a doubling of all flows in leads to a doubling of U. Then the real value of consumption measures ut­ility:

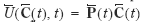
, where

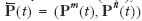
It seems to be associated with large informational demands to include the fixed or non-measurable components Cⁿ in the consumption vector. (However, Weitzman, 2001, shows how these informational demands can be satisfied by estimating a change in ‘consumers’ surplus’, which in principle is observable.)

If we make the additional technological assumption of constant returns to scale , then national wealth can be measured by the value of the current capital vector. This assumption can be interpreted as follows: The set of attainable consumption-investment pairs does not only depend on variable and measurable capital components K^m, but also fixed or non-measurable components Kⁿ, so that the set of attainable consumption-investment pairs at time t equals

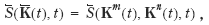
where a doubling of all stocks in

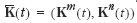
means that all consumption and investment flows can be doubled as well. Then the real value of the current capital vector measures national wealth:

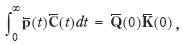
where

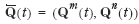
It seems to be associated with large informational demands to include the fixed or non-measurable components Kⁿ in the capital vector. Fixed capital components play no role in Weitzman’s theory of national accounting, as he does not impose an assumption of constant returns to scale.

Hence, the problems associated with using national wealth as an aggregate indicator of welfare improvement and sustainability are two-fold:

1. The consumption vector must include not only variable but also fixed components in order for the consumption price index to allow for comparisons of real wealth over time (otherwise, changed relative scarcity of these fixed consumption components will not be taken into account).

2. The capital vector must include not only variable but also fixed components in order for the value of the capital vector to account for all future consumption flows (otherwise, welfare significant capital gains or losses on these fixed capital components will not be included).

To include such fixed consumption and capital components is a demanding task in a setting where environmental amenities and natural capital are important. On the other hand, when national wealth is used as an indicator of welfare improvement and sustainability, it does not represent an additional problem that the function U and the set S depend directly on time as well, since anticipated capital gains will capture the effects of changes in society’s productive capacity.

It might be useful to end this discussion of national wealth as an indicator with a reminder:

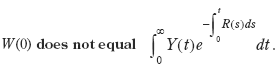
Since Y ( t ) includes the value of net investments, it follows from the definition of national wealth at the beginning of this section that the present value of future comprehensive NNP would overestimate national wealth if the value of net investments is positive throughout. Therefore, it is of no interest to calculate the present value of future comprehensive NNP. This also means that it is of no interest to calculate the present value of future real returns on the capital components even under the assumptions of a constant real interest rate and constant returns to scale (which are assumptions under which Y ( t ) equals the real returns on the capital components). If we would want to calculate national wealth by calculating wealth for different kinds of capital components (human capital, reproducible capital, different kinds of natural capital, etc.), this should be done by calculating the present value of future cash flows for the different capital components, not by calculating the present value of the future real returns on the capital components. It might also important to warn against calculating the value of human capital by assuming sustained productivity growth. Due to the importance of labor in the functional distribution of income, this amounts to assuming future welfare improvement and sustainability rather than trying to construct indicators for this purpose.

3.5 Population growth

The conclusions of Sections 2 and 3 carry over to the case where there is population growth.

Also with population growth, dynamic welfare is increasing if and only if the present value of future changes in comprehensive consumption is positive , provided that (1) the instantaneous well-being of the society equals total utility, i.e., per capita utility times population size, and (2) instantaneous well-being is unchanged if an additional person is brought into society and the total consumption flows must be spread on the additional person.

Also with population growth, the present value of future changes in comprehensive consumption can be measured by a genuine savings indicator and growth in real comprehensive NNP , as long as the value of net investments includes the value of current population growth (which, in turn, can be measured as the present value of the product of future wages and future population growth).

Hence, per capita measures need not be considered. Simple per capita measures can be used to indicate welfare improvement and sustainability only if the technology exhibits constant returns to scale and population growth is assumed to remain exponential for an indefinite future. While the former assumption is strong (cf. Section 4), the latter assumption is neither sensible in a finite world nor realistic given the current population trends. Arrow et al. (2003b) and Asheim (2004) are two recent contributions on comprehensive national accounting with population growth.

3.6 Imperfect resource allocation

In Sections 2–5 I have had in mind the situation in a well-functioning and developed society and assumed that resource allocation is optimal. On the other hand, I have not insisted that the objective of society is to maximize the sum of discounted utilities. In contrast, Dasgupta and Mäler (2000), Dasgupta (2001), and Arrow et al. (2003a) assume that society adheres to a discounted utilitarian welfare function, but possibly allocates resources in an imperfect way. They thereby model (i) the pervasive inefficiencies that are observed in many developing countries and (ii) the inefficient management of natural and environment resources in societies that are otherwise quite efficient.

Let calculated consumption prices be proportional to the partial derivatives of the utility function U, and let calculated investment prices be proportional to the partial derivatives of the state valuation function

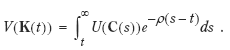
Then the results of Sections 2 and 3 go through (see Asheim, 2003, Sect. III): Also with imperfect resource allocation, (i) welfare improvement corresponds to a positive present value of future changes in comprehensive consumption, and (ii) a positive present value of future changes in comprehensive consumption corresponds to both a positive genuine savings indicator and growth in real comprehensive NNP.

However, Pezzey’s (2004) one-sided sustainability test does not hold if resource allocation is imperfect. Consider, e.g., a society where traditional growth is promoted through high investment in reproducible capital goods, but where incorrect (or lack of) pricing of natural capital leads to depletion of natural and environmental resources that is excessive both from the perspective of short-run efficiency and long-run sustainability. Then utility growth in the short to intermediate run may lead to current growth in dynamic welfare. If so, both the genuine savings indicator and real NNP growth are positive. Still, the depletion of natural capital may seriously undermine the long-run livelihood of future generations, so that current utility far exceeds the level that can be sustained forever.

Moreover, the analysis of Section 4 does not go through, as national wealth cannot be measured by the value of the current capital vector if resource allocation is imperfect, even if we make the additional assumption of constant returns to scale.

3.7 Methods for satisfying informational demands

We must be able to account for changes in society’s productive capacity, i.e., changes caused by

• accumulation of ordinary reproducible capital,

• technological change and human capital accumulation,

• reduced availability of natural and environmental resources,

• in the case of open economies, changing terms-of-trade.

As discussed in Section 3, comprehensive accounting entails that all such changes in society’s productive capacity are captured by the vector of investments flow, where the size of these flows can be measured and valued at market or calculated accounting prices. What can be done if the assumption of comprehensive accounting is not satisfied, so that it is not the case that all changes in society’s productive capacity correspond to stock changes that can be measured and valued?

One–purely formal, but in principle important–method consists of letting time be an additional state variable–i.e., an additional capital component–as we have already indicated in Section 3. This reformulates the problem as one of measuring the ”value of passage of time”.

A first attempt at a practical solution is to assume that the value of passage of time does not change over time . Then time does not contribute to changes in the value of net investments. Hence, time need not be included when calculating growth in real NNP. On the other hand, one must calculate how the real value of consumption changes over time, where the consumption vector must include, e.g., environmental amenities.

Growth in real NNP will also give a right qualitative result if the value of passage of time is in fixed proportion to total NNP. The Dasgupta-Heal-Solow model (Dasgupta and Heal, 1974, 1979; Solow, 1974) of capital accumulation and resource depletion illustrates this possibility: With fixed factor shares, the value of resource depletion is a fixed proportion of comprehensive NNP. Therefore, real NNP growth measures welfare improvement even if resource depletion is not included, while the measurable value of net investments can be grossly inaccurate if resource depletion is left out.

Another possibility is illustrated by a model where technological progress is endogenous, in the sense that human capital accumulation equals the fraction of net output that is used for neither consumption nor accumulation of ordinary reproducible capital. Assume that net output (= real NNP) is observable, but that it is not possible to observe how net output not used to augment the stock of ordinary capital is split between consumption, on the one hand, and investment in human capital, on the other. Then, real NNP growth can be used for indicating welfare improvement (and sustainability), while the sign of the measurable value of net investments may not indicate correctly since human capital accumulation cannot be distinguished from consumption.

A second attempt at a practical solution is to try directly to measure the value of passage of time, using forward-looking terms . Such methods have been suggested by e.g. by Aronsson and Löfgren (1993), Pezzey (2004), Sefton and Weale (1996), and Vellinga and Withagen (1996). In particular, Sefton and Weale (1996) show how to take into account changing terms-of-trade being faced by a natural resource exporter.

A third attempt at a practical solution to capture the effects of changes in society’s productive capacity by means of anticipated capital gains . As mentioned in Section 4, this requires that one can assume a constant interest rate and constant returns to scale. Then anticipated capital gains will capture the effects of changes in society’s productive capacity, as mentioned in Section 4. When using this method, one must, as mentioned in Section 4, face the practical problems that arise when trying to satisfy the assumption of constant returns to scale. These problems are especially serious in a world where natural and environmental resources are important. Moreover, unanticipated (”windfall”) capital gains as well as capital gains arising from changing interest rates must be excluded. The method seems to be of practical interest when estimating the sustainable income arising from a raw material exporting country’s natural resource endowment.

References

Aronsson, T. and Löfgren, K.-G. (1993), Welfare consequences of technological and environmental externalities in the Ramsey growth model. Natural Resource Modeling7, 1–14.

Arrow, K., Dasgupta, P.S., and Mäler, K.-G. (2003a), Evaluating projects and assessing sustainable development in imperfect economies. Environmental and Resource Economics26 , 647-685.

Arrow, K.J., Dasgupta, P.S., and Mäler, K.-G. (2003b), The genuine savings criterion and the value of population. Economic Theory21 , 217–225.

Asheim, G.B. (1994), Net national product as an indicator of sustainability. Scandinavian Journal of Economics96 , 257–265.

Asheim, G.B. (2003), Green national accounting for welfare and sustainability: A taxonomy of assumptions and results. Scottish Journal of Political Economy50 , 113–130.

Asheim, G.B. (2004), Green national accounting with a changing population. Economic Theory23 , 601–619.

Asheim, G.B. and Weitzman, M.L. (2001), Does NNP growth indicate welfare improvement? Economics Letters73 , 233–239.

Dasgupta, P.S. (2001), Valuing objects and evaluating policies in imperfect economies. Economic Journal111 , C1–C29.

Dasgupta, P.S. and Heal, G.M. (1974), The optimal depletion of exhaustible resources. Review of Economic Studies (Symposium), 3–28.

Dasgupta, P.S. and Heal, G.M. (1979), Economic Theory and Exhaustible Resources. Cambridge University Press, Cambridge, UK.

Dasgupta, P.S. and Mäler, K.-G. (2000), Net national product, wealth, and social well-being. Environment and Development Economics5 , 69–93.

Dixit, A., Hammond, P., and Hoel, M. (1980), On Hartwick’s rule for regular maximin paths of capital accumulation and resource depletion. Review of Economic Studies47 , 551–556.

Hamilton, K. (1994), Green adjustments to GDP. Resources Policy20 , 155–168.

Heal, G.M. and Kriström, B. (2003), National income and the environment. Forthcoming in Mäler, K.-G. and Vincent, J. (eds.), Handbook of Environmental Economics, North-Holland, Amsterdam.

Pezzey, J.C.V. (2004), One-sided sustainability tests with amenities and changes in technology, trade and population. Journal of Environmental Economics and Management48 , 613–631.

Samuelson, P. (1961), The evaluation of ‘social income’: Capital formation and wealth. In The Theory of Capital (eds. Lutz, F.A. and Hague, D.C.), pp. 32–57. St. Martin’s Press, New York.

Sefton, J.A. and Weale, M.R. (1996), The net national product and exhaustible resources: The effects of foreign trade. Journal of Public Economics61 , 21-47.

Solow, R.M. (1974), Intergenerational equity and exhaustible resources. Review of Economic Studies (Symposium), 29–45.

Vellinga, N. and Withagen, C. (1996), On the concept of green national income. Oxford Economic Papers48 , 499–514.

Weitzman, M.L. (1976), On the welfare significance of national product in a dynamic economy. Quarterly Journal of Economics90 , 156–162.

Weitzman, M.L. (2001), A contribution to the theory of welfare accounting. Scandinavian Journal of Economics 103, 1–23.