7 Lillestrømulykken, brannteknisk analyse
Computational Industry Technologies AS (ComputIT)
B.F. Magnussen, T. Evanger, N.I. Lilleheie og T.E. Hals
Sammendrag
Rapporten omfatter en analyse av det aktuelle hendelsesforløpet i forbindelse med brannen som oppstod mellom to propantankvogner ved togkollisjonen på Lillestrøm i april 2000. I tillegg omfatter rapporten en analyse av andre mulige hendelsesforløp.
For den aktuelle ulykken er hovedkonklusjonen at når en sammenholder simuleringer, beregninger og observasjoner og tar i betraktning usikkerheter, er det sannsynlig at flytekapasiteten for beholdermaterialet i det brannutsatte området på fremre vogn ble overskredet etter ca. 2 timers brann. Det var kritisk viktig å nedkjøle tankene med vann, og dette forhindret med stor sannsynlighet en videre utvikling mot katastrofe. Dette var en alvorlig ulykke hvor i hovedtrekk de riktige katastrofehindrende tiltak ble gjort.
Simuleringer av brannsituasjoner med andre vindforhold og større lekkasjerater, viser at dersom ulykken hadde hatt et annet forløp, som i seg selv ikke er usannsynlig, ville flytekapasiteten for fremre vogn sannsynligvis kunne blitt overskredet til dels mye tidligere enn i det virkelige tilfellet. I så fall ville ulykken kunne utviklet seg mot en katastrofe i løpet av relativt kort tid.
Analysen av konsekvensen av gasslekkasje uten antennelse viser at gassen i det gjeldende tilfellet ville bli raskt uttynnet. Dette forteller oss at flammen sannsynligvis med fordel kunne ha vært slukket.
Beregninger viser at en eksplosjon og ødeleggelse av en eller begge tankene ville ført til en formidabel ildkule med katastrofale konsekvenser.
ComputITs rapport har tre appendikser A – C. Appendiks A er inntatt. Appendiks B «Tidsutvikling av ildkule simulert med Kamelon FireEx» og appendiks C «Kamelon FireEx» har Kommisjonen ikke funnet det hensiktsmessig å innta.
Sammendrag
Rapporten omfatter en analyse av det aktuelle hendelsesforløpet i forbindelse med brannen som oppstod mellom to propantankvogner ved togkollisjonen på Lillestrøm i april 2000. I tillegg omfatter rapporten en analyse av andre mulige hendelsesforløp.
Analysen er basert på detaljerte numeriske simuleringer med dataprogrammet Kameleon FireEx (KFX), utviklet ved NTNU/SINTEF av professor Bjørn F. Magnussen og hans medarbeidere.
Hovedkonklusjonen av analysen er at i hovedsak ble de riktige tiltak iverksatt, men under mer ugunstige forhold kunne ulykken ha fått et dramatisk forløp. I det aktuelle tilfelle var lekkasjeraten av propan sannsynligvis ca. 150 g/s, tilsvarende 540 kg/time. Fremre vogn var særlig utsatt fordi den hadde fått en skråstilling som konsekvens av kollisjonen slik at væskenivået i tanken mot brannen ble liggende relativt lavt. Derved oppstod det et stort område i den branneksponerte enden av tanken hvor stålmaterialet ble opphetet, sannsynligvis opp mot ca. 690 °C. Dette førte til en betydelig svekkelse av materialets styrke samtidig med en betydelig trykkstigning inne i tanken.
Når en sammenholder beregninger og observasjoner og tar i betraktning usikkerheter, er det sannsynlig å fanta at flytekapasiteten for beholdermaterialet i det brannutsatte området på fremre vogn ble overskredet etter ca. 2 timers brann.
Overrislingen av tankene med vann som startet etter ca. 2 timer, forhindret utviklingen mot en katastrofe.
Simulering av en rekke alternative situasjoner viser at en var svært heldig. Dersom lekkasjeraten hadde vært større og det hadde blåst sterkere vind, eller at omgivelsestemperaturen hadde vært høyere, ville brudd i tankene ha kunnet finne sted i løpet av ca. en halv time etter antennelse.
Hvis en tank hadde eksplodert ville det ha blitt dannet en ildkule med diameter ca. 200 m som ville ha ført til ekstrem termisk stråling i et område med 500–1000 m utstrekning. Selv om varigheten ville ha vært kort, sannsynligvis av størrelsesorden 10 sekunder, ville konsekvensene ha vært dramatiske. Med stor sannsynlighet ville også den andre tanken ha eksplodert med tilsvarende større omfang på ulykken.
En kan med utgangspunkt i den gjennomførte analyse konkludere med at de katastrofehindrende tiltak som ble iverksatt i hovedsak var riktige, herunder at tankene ble overrislet med vann, at tankene ble tømt, og at befolkningen ble evakuert.
Det er klart at vannoverrislingen ble iverksatt i høy tid, og at den burde ha startet tidligere.
Analysen av konsekvensen av gasslekkasje uten antennelse viser at gassen i det angjeldende tilfellet ville bli raskt uttynnet. Dette forteller oss at flammen sannsynligvis med fordel kunne ha vært slukket.
Det er klart at det ikke er lett under eksisterende ulykkessituasjon å vite hvilke løsninger en skal velge. Med det eksisterende simuleringsverktøy (KFX) vil en imidlertid kunne simulere en rekke alternative situasjoner og på denne bakgrunn utvikle et sett med retningslinjer for forebyggende tiltak og redningsarbeid. Når en tar i betraktning all transport av gass i tankvogner på jernbane og vei som finner sted, og at ulykker med stor sannsynlighet vil skje, vil vi anbefale at det iverksettes prosjekt for å utvikle slike retningslinjer.
7.1 Introduksjon, bakgrunn
I april 2000 kolliderte to togsett på Lillestrøm stasjonsområde. Det ene togsettet fraktet propan på tankvogner, og ved kollisjonen støtte to tankvogner sammen med propanlekkasje og brann som følge.
Brannen pågikk over flere dager mens det parallelt ble arbeidet med avgrensning av brannkonsekvensene gjennom overrisling av tankene med vann, og avfakling av propanen for å få tømt tankene. Situasjonen ble med rette betraktet som svært alvorlig, og store områder ved Lillestrøm stasjon ble avsperret, og hele befolkningen i området evakuert i flere dager mens brannen pågikk. Tiltakene som ble satt inn og redningsarbeidet var vellykket, tankene ble tømt uten at de kollapset og brøt sammen, og uten at eksplosjon eller en fireball oppstod.
Ulykken kunne imidlertid fått et langt alvorligere utfall, og i etterkant av ulykken ble prosjektet som rapporteres her igangsatt. Formålet med studien er å finne ut hvilke marginer en hadde i ulykken, hvor nært katastrofen en var, betydningen av de eksterne innsatsfaktorer og lignende, samt å gjennomføre en sensitivitetsanalyse for de viktigste parametre i denne sammenhengen. I tillegg til å etablere kunnskap om den aktuelle ulykken og hendelsesforløpet der, er det en viktig del av studien å få frem kunnskap om hvordan utviklingen ville ha vært dersom ulykkesbildet hadde vært litt annerledes, om propanen ikke hadde blitt antent eller lignende, med tanke på å trekke lærdom av hendelsen for bruk i eventuelle senere sammenhenger, opplæring av personell osv.
Katastrofen ble avverget i denne ulykken, men ulykkestilfellet er svært interessant fordi en på basis av observasjoner under og etter brannen sammenholdt med beregninger og simuleringer som blir gjort i studien, vil kunne trekke vidtrekkende konklusjoner med stor grad av sikkerhet. Dette vil kunne være av stor betydning med tanke på bruke ulykken som basis for fremtidig sikkerhetsarbeid.
Prosjektet består i to hoveddeler:
Modellering og simulering av lekkasje, brannforløp og temperatur- og spenningsutvikling i tankene i den aktuelle ulykken
Gjennomføring av en sensitivitetsanalyse for å fremskaffe informasjon om konsekvenser av et annerledes ulykkesbilde som for eksempel andre lekkasjerater, andre vindforhold, at propanen ikke blir antent og sprer seg utover et større område som tung gass, av at beholdere revner med fireball som følge og lignende. Alt dette som underlag for videre arbeid med retningslinjer for både forebyggende tiltak og eventuelt senere redningsarbeid
Den foreliggende rapporten sammenfatter resultatene fra begge deler av studien.
7.2 Generell diskusjon av problemstillingen
Ved kollisjonen ble de to tankvognene som transporterte propan presset mot hverandre slik at det oppsto lekkasje i flensene for mannhullene på de to vognene. Mannhullene var vendt mot hverandre og de ble stående i nær kontakt med hverandre.
Vognene var fylt med propan, og væskenivået i tankene når tankene stod horisontalt nådde en høyde fra bunnen på ca. 2,17 m. Diameteren på tankene var 3,0 m. Dette betyr at når vognene stod horisontalt ville det bare være gass helt øverst i tanken.
Forholdet var at bakre vogn ble stående horisontalt mens fremre vogn fikk en skråstilling på 5° målt i vognens lengderetning, med det høyeste punkt vendt mot bakre vogn. Dette innebærer at som vist i figur 7.1 at gassområdet strakk seg til like under senterplanet for tanken.
For begge vognene lå imidlertid lekkasjepunktet godt under væskenivået, slik at lekkasjetverrsnittet ble gjennomstrømmet av propan væske.
Omtrent 5 minutter etter sammenstøtet mellom de to vognene ble gassen som lakk ut antent og det oppstod brann mellom vognene. Hvor stor lekkasjemengden i de to flensene til sammen var er ukjent, men vi kan regne med at den var i området 50 g/s til 150 g/s (cfr. kap. 3.1.2 og 3.1.3). Dette er i seg selv en begrenset mengde, men dette tilsvarer imidlertid 2.3 MW til 6.9 MW. Altså en meget betydelig varmeutvikling.
Ved forbrenning av propan med luft utvikles det svært høye temperaturer inne i flammen, med maksimaltemperaturer i området 1700 °C til 1900 °C. Når gass ved slike høye temperaturer berører metallet i tankene blir det overført varme ved såkalt konvektiv varmeoverføring. Den største varmeoverføring til tankene skjer imidlertid ved varmestråling. Denne strålingen kommer fra gasskomponenter som CO2 og H2 O i flammen, men det største strålingsbidraget kommer imidlertid fra glødende sotpartikler. Sotpartiklene er ansvarlig for det gult lysende i flammer og dannes under selve forbrenningsprosessen. Våre beregninger viser, som vi skal komme tilbake senere i rapporten, at inne i flammen som oppstod mellom vognene har det vært strålingsflukser på over 100 kW pr. m2. Altså over 100 ganger så sterk som strålingen fra solen på en solskinnsdag ved ekvator.
Selv om noe av strålingen dempes før den når beholderne, vil betydelige varmemengder overføres til disse.
Varmeoverføringen fra flammene fra brannen mellom vognene har to konsekvenser. Den ene er at propanen i beholderne varmes opp slik at trykket i beholderne stiger, noe som igjen fører til at materialspenningene i beholderveggene øker. Dette er et faremoment i seg selv fordi beholderne er konstruert for å kunne tåle et bestemt trykk under normale temperaturer. Lekkasjen fra flensene bidrar prinsipielt til at trykket ikke stiger så raskt. Men i dette tilfelle var dette bidraget neglisjerbart. 150 g/s tilsvarer 540 kg/time, mens tankenes totale innhold var ca. 43 tonn hver.
Den andre konsekvensen av varmeoverføringen er at stålmaterialet i tankene varmes opp. Hvis stålmaterialet varmes opp til ca. 500 °C vil styrken reduseres med ca. 55 %, mens ved en temperatur på ca. 700 °C vil styrken i materialet være redusert til i området 20–15 % av den opprinnelige styrke. Et slikt tilfelle kombinert med tilstrekkelig trykkoppbygning inne i beholderen ville kunne få den katastrofale følge at beholderen ville briste, med påfølgende ekstrem brannutvikling.
I dette tilfelle er det materialet i beholderen som befinner seg i gassområdet over væskespeilet som vil være mest utsatt for slik oppvarming. I væskeområdet vil materialtemperaturen holde seg i nærheten av propanvæskens temperatur fordi propanvæsken så effektivt vil føre varmen bort fra veggen og inn i propanen. I gassområdet er imidlertid varmeoverføringen inne i beholderen vesentlig mindre. Gassen er ikke i stand til å føre varmen fra materialet inn i væsken slik at materialtemperaturen stiger inntil ny likevekt mellom tilført og bortført varme oppnås. Dette vil, avhengig av varmeoverføringen fra brannen, føre til temperaturer som indikert.
Som konsekvens av dette er det fremre vogn, den vognen som hadde det laveste væskenivå, som var mest utsatt. Våre observasjoner av vognene etter ulykken viser at en utbuling av beholderen på fremre vogn hadde funnet sted, noe som indikerer at en har vært i faresonen.
Etter ca. 2 timer begynte en å overrisle tankene med vann uten å berøre selve flammene i vesentlig grad. Vannmengden var begrenset, ca. 1600 kg/min. pr. vogn, men en kan regne med at fra dette tidspunkt ble det bortført så mye varme fra tankene gjennom vannet at trykkstigningen opphørte. Muligens falt trykket i tankene etter dette tidspunkt. Eksempelvis vil en temperaturstigning på vannet på ca 1 °C kunne transportere bort 110 kW. Sannsynligvis var varmetilførselen til tanken på fremre vogn av størrelsesorden 300 kW (cfr. senere deler av rapporten).
Hvis en i denne fase hadde slukket brannen ville uforbrent gass ha sluppet ut. Konsekvensen av dette er ikke lett å forutsi. Dette forhold vil imidlertid bli belyst i senere deler av denne studien.
Tankene ble fornuftigvis tømt relativt raskt ved fakling etter tilkopling av tømmeledninger. Generelt er det viktig å ha i mente at tankene var særlig utsatt under denne prosessen på grunn av det synkende væskenivået.
De forhold som vi her har drøftet i en generell form vil bli nærmere belyst i den foreliggende rapporten.
7.3 Ulykkesscenariet
7.3.1 Startbetingelser
7.3.1.1 Propantankenes innhold og dimensjoner
Figur 7.1 viser propantankens dimensjoner og væskenivå.
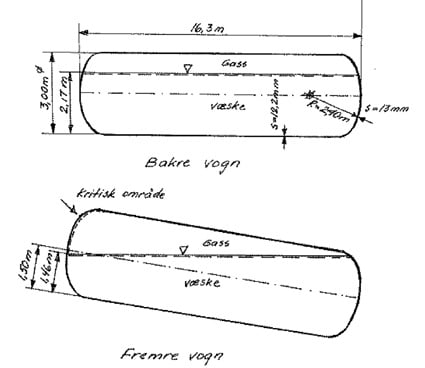
Figur 7.1 Vognenes geometri og væskenivå
Tankene var fylt med henholdsvis 83.8 m3 og 85.4 m3 propan 95. Dette tilsvarer ca. 43 tonn propan i hver av tankene.
Temperaturen i beholderne antas å ha vært 5 °C før kollisjonen. Det tilsvarende trykk er 5.5 bar absolutt, altså 4.5 bar overtrykk.
Propan 95 inneholder typisk 1 % etan (C2 H6 ), 95 % propan (C3 H8 ), og ca. 1 % pentener (C5 H12 ).
7.3.1.2 Inngangsdata for beregningene
Lekkasjearealet fra tankene har vært forsøkt bestemt i ettertid gjennom luftgjennomstrømnings-analyser (ref.1).
Lekkasjenes lokalisering har vært bestemt ved termografiske undersøkelser av de skadde tankene (ref. 2).
Da det er tvil om i hvilken grad det har vært lekkasje under brannen i alle angitte lekkasjepunktene i ref. 1, har vi i samråd med våre oppdragsgivere valgt å konsentrere oss om lekkasjene i forbindelse med mannhullene for de to tankene, og den lokalisering av lekkasjepunktene som ble bestemt i ref. 2. Det var også mellom tankene brannen utviklet seg.
For fremre vogn er det usikkerhet med hensyn til hvor stor del av lekkasjen som kan henvises til flensen på mannhullet, og til lufteplugg på toppen i samme ende som flensen. Som utgangspunkt har vi henført lekkasjearealet til flensen.
Med dette som bakgrunn har vi tatt utgangspunkt i følgende inngangsdata, se tabell 7.1.
Tabell 7.1 Inngangsdata for simuleringene
| Lekkasjeareal tank fremre vogn | 1.22 mm2 |
| Lekkasjeareal tank bakre vogn | 1.9 mm2 |
| Propan lekkasjerate totalt for tankene | 45 g/s |
| Start temperatur i propantankene | 278 K (5 °C) |
| Start trykk i propantankene | 4.5 barg |
| Vindretning | Parallelt med togakse |
| Vindhastighet | 1.5 m/s 10 meter over bakken (svak vind) |
Lekkasjepunktene er plassert i toppen av flensen på enden av tankene. Lekkasjen er modellert svakt usymmetrisk slik at flammen bøyer av litt mot høyre sett mot fremre vogn i vindretningen, og det er tatt hensyn til at lekkasjepunktene er noe forskjøvet i høyderetningen for de to tankene.
7.3.1.3 Lekkasjemengden
Lekkasjearealene i ref. 1 ble bestemt ved å måle tilført luft samtidig som trykket i beholderen ble holdt konstant. Trykket i beholderne under testen var typisk i området 1.55 bar absolutt til 1.35 bar absolutt tilsvarende 0.55 bar og 0.35 bar overtrykk, og temperaturen i området 12°C til 21°C.
Lekkasjearealet ble beregnet etter følgende formel:
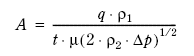
Figur 7.2
hvor:
q = m3 luft inn over perioden
ρl = spes. vekt atmosfæreluft
t = tiden av perioden
µ = faktor (pga. lekkasjepunktenes geometri er den valgt til 0,7)
ρ2 = spes. vekt for «tankluft»
Δp = trykkforskjell mellom tank og atmosfære
Hvis vi innfører massestrømmen,
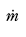
Figur 7.3
i uttrykket fås:
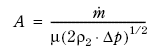
Figur 7.4
Ved å omforme dette uttrykket finner vi uttrykket for massestrømmen:
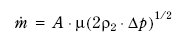
Figur 7.5
eller
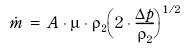
Figur 7.6
Dette er et uttrykk som er gyldig for strømning over en restriksjon.
Lekkasjen i flensen for mannhullene er sannsynligvis forbundet med en relativt kompleks strømning i smale spalter og gjennom små hull. Det er derfor høyst tvilsomt om det anvendte utrykk (1) er gyldig. Vi har derfor valgt å betrakte arealet, A, som en fiktiv størrelse og beregnet massestrømmen, lekkasjemengden
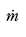
Figur 7.7
, ved å benytte uttrykk (3). Altså i prinsipp det samme uttrykk som i (1) og med samme koeffisienter, men med relevante data for flytende propan 95.
Når vi benytter relevante data for tankene (jf. tabell 7.1, Inngangsdata) får vi en samlet lekkasjemengde i spalten mellom de to vognene på:
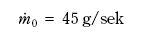
Figur 7.8
En ser av uttrykk (3) at lekkasjemengden stiger når trykket i beholderen stiger slik at når for eksempel overtrykket i beholderen dobles, vil lekkasjemengden,

Figur 7.9
, øke med ca. 40 %.
Problemstillingen kompliseres ytterligere av at lekkasjearealet er bestemt under kald tilstand i ettertid ved et overtrykk i størrelsesorden 10 % av overtrykket i beholderen under brannen. Det vil ikke være urimelig å anta at lekkasjearealet kan ha vært trykkavhengig. Altså større under den aktuelle brannsituasjonen.
Med dette som bakgrunn har vi valgt følgende strategi for beregningene:
Det gjennomføres tre beregningstilfeller for brannen med følgende lekkasjemengder:
Tilfelle A:

Figur 7.10
Tilfelle B:
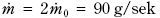
Figur 7.11
Tilfelle C:
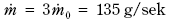
Figur 7.12
Det mest realistiske brannscenariet fastlegges deretter ved å sammenholde beregningsresultatene med observasjoner under og etter brannen.
Vi har valgt å holde en fast lekkasjerate for propanen på grunn av usikkerheten som er forbundet med fastsettelsen av raten.
7.3.1.4 Atmosfæriske forhold
Vindforholdene har betydning for flammeutviklingen. Vi har valgt å gjennomføre beregningen med en vindhastighet på 1,5 m/s parallelt med vognene og i retning mot fremre vogn. For øvrig er det antatt 0 °C i omgivelsene.
7.3.2 Brannutviklingen og materialtemperaturer
7.3.2.1 Tankveggenes oppvarming
Oppvarmingsproblemstillingen karakteriseres av figur 7.2.
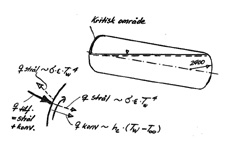
Figur 7.13 Oppvarmingsproblemstillingen
Tankenes yttervegger utveksler varme med omgivelsene, herunder flammen, gjennom stråling og konveksjon. Samtidig transporteres varme inn i propanen gjennom tilsvarende mekanismer.
I væskeområdet er varmeovergangen meget effektiv. Derfor vil beholderens veggtemperatur i dette området alltid ligge i nærheten av propanens temperatur.
I gassområdet er varmeovergangen mindre effektiv slik at beholderveggen kan anta temperaturer som ligger nærmere flammenes temperatur. Derfor er dette området spesielt utsatt under brann.
Figur 7.3 viser veggtemperaturen i gassområdet som funksjon av netto varmefluks på veggens ytterside.
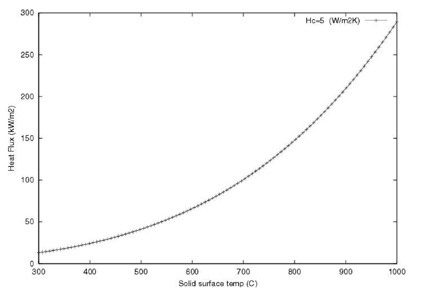
Figur 7.14 Typisk utvikling av veggtemperatur i gassområdet som funksjon av netto varmefluks på en brannbelastet tanks ytterside
En varmefluks på 50 kW/m2 gir en veggtemperatur på 525 °C, mens 100 kW/m2 gir 700 °C. Disse forholdene er inkludert i Kameleon FireEx og ivaretatt i de beregningene som omtales i det følgende.
7.3.2.2 Brannsimuleringene
Brannsimuleringene utføres med Kameleon FireEx. Dette er et generelt simuleringsprogram for forbrenning, spesielt rettet mot brann. Programsystemet tar utgangspunkt i grunnlikningene for strømning, termodynamikk, varme- og masseoverføring, kjemiske reaksjoner, og inkluderer modeller for fysikalske delprosesser.
Kameleon FireEx kan simulere transient brannutvikling i det tredimensjonale rom, hvor innflytelse av konstruksjoner og konstruksjonselementer kan inkluderes. Programsystemet er ut-viklet ved NTNU/SINTEF-varmelæremiljøet over en 25 års periode, de siste 5 årene i nært samarbeid med Statoil, Elf, Ruhrgas, Gaz de France og ENI-gruppen (Snam og Agip). Alt ansvar for programsystemet, inklusiv videreutvikling, er nå overtatt av ComputIT. Programmet er omfattende testet og har for øvrig operasjonelle egenskaper som er unik i internasjonal sammenheng (se for øvrig appendiks B).
Med Kameleon FireEx beregner vi både selve brannutviklingen, varmeoverføringen til tankene, og materialtemperaturene i tankveggene.
Det er gjennomført simuleringer for de tre lekkasjetilfellene:
A:
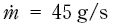
Figur 7.15
B:

Figur 7.16
C:

Figur 7.17
Vind blåser parallelt med toget med retning fra bakre vogn mot fremre vogn.
Figur 7.4 (a, b, c og d) viser resultatene for tilfelle A.
Figur 7.4a viser de maksimale temperaturene i flammen sett inn mot fremre vogn, mens figur 7.4b viser brannen sett fra siden.
Figur 7.4c viser den maksimale strålingsfluksen fra flammen inn mot fremre vogn. Figur 7.4d viser ståltemperaturene i den enden av fremre tank som vender inn mot spalten mellom vognene.
Figurene 7.5 viser tilsvarende for tilfelle B, mens figurene 7.6 viser tilsvarende for tilfelle C.
Figur 7.7 viser «ray-tracing» bilder, dvs bilder som avbilder flammene sett utenfra for de tre beregningstilfellene.
Noen karakteristiske resultater fra beregningene er sammenstilt i tabell 7.2.
Tabell 7.2 Karakteristiske resultater fra Kameleon FireEx beregningene
| Tilfelle | Lekkasjerate (g/s) | Vind (m/s) | Utviklet varme (kW) | Maks flamme- temperatur (°C) | Maks strålingsfluks inn mot fremre vogn (kW/m2 ) | Maks ståltemperatur tank fremre vogn (°C) |
|---|---|---|---|---|---|---|
| A | 45 | 1.5 | 2087 | 1869 | 77 | 526 |
| B | 90 | 1.5 | 4174 | 1876 | 107 | 650 |
| C | 135 | 1.5 | 6261 | 1682 | 130 | 690 |
Maksimal flammetemperaturer som angitt i tabell 7.2 er hentet fra a og b i figurene 7.4 til 7.6. Maksimal strålingsfluks inn mot fremre vogn er hentet fra c i figurene 7.4 til 7.6, mens maksimal ståltemperatur er hentet fra d i figurene 7.4 til 7.6.
Maksimal ståltemperatur slik som det fremkommer her er lavere enn hva som indikeres i fra figur 7.3. Dette skyldes at netto varmefluks er lavere enn den maksimale strålingsfluksen, blant annet på grunn av tilbakestråling fra veggen. Materialtemperaturene som er angitt er de som er fremkommet etter at stasjonære forhold har inntrådt.
En ser også at de høye overflatetemperaturene opptrer i gassområdet for tanken. Under væskenivået er overflatetemperaturene lave og ikke svært avvikende fra væsketemperaturen i beholderne.
Når vi sammenholder beregningsresultatene i figur 7.4 til 7.7 med fotografier av selve brannen, figur 7.8, samt spor på fremre vogn, figur 7.9 og 7.10, synes beregningstilfelle C med lekkasjeraten 135 g/s å gi et brannbilde som samsvarer godt med observasjonene.
Av særlig betydning i dette tilfelle er at det er først ved denne lekkasjemengden at vi beregningsmessig observerer flammer i underkant av tanken.
En må selvsagt ved slike vurderinger ta i betraktning at selv om beregningene med stor sannsynlighet er riktige, vil de alltid være beheftet med unøyaktigheter.
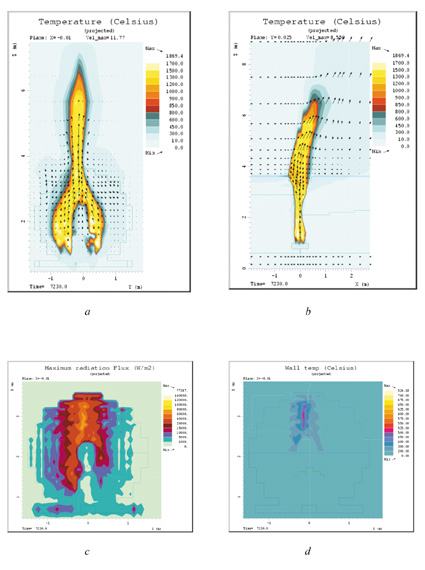
Figur 7.18 Beregningsresultater for tilfelle A, lekkasjerate 45 g/s
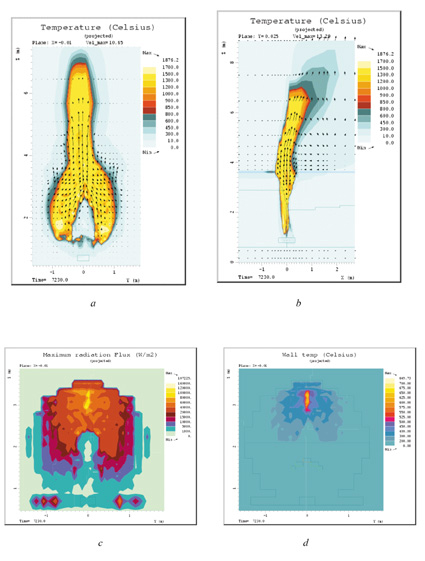
Figur 7.19 Beregningsresultater for tilfelle B, lekkasjerate 90 g/s
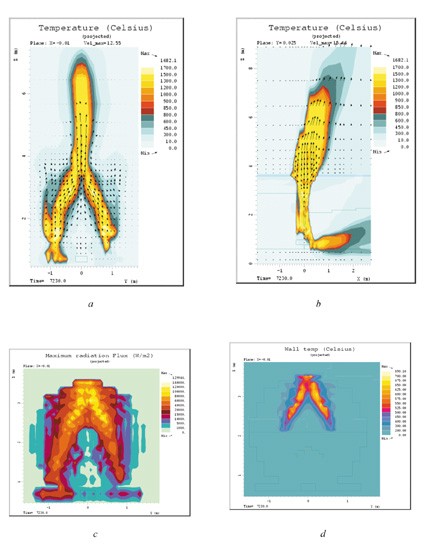
Figur 7.20 Beregningsresultater for tilfelle C, lekkasjerate 135 g/s
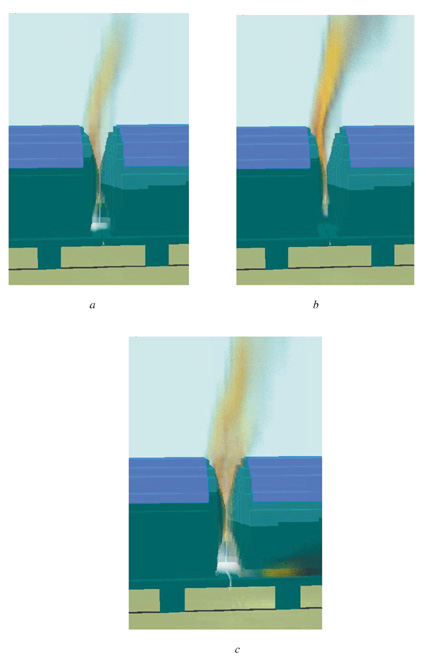
Figur 7.21 Ray-tracing bilder av de beregnede flammene, tilfelle A, B og C

Figur 7.22 Fotografi av brannen
Kilde: Scanpix

Figur 7.23 Fotografi av fremre vogn med merker etter brannen
7.3.3 Trykkutvikling i tanken
Når propantankene utsettes for brannbelastning fører det til trykkstigning i beholderne dersom trykkavlastningen, dvs utstrømningsraten, ikke er så stor at den dominerer over trykkøkningen som er en følge av varmetilførselen. For den aktuelle situasjonen er utstrømningsraten liten, 45–135 g/s samlet for tankene. Virkningen på trykkstigningen av lekkasjen er derfor liten. Trykknivået som funksjon av tid er av sentral betydning idet kapasiteten til materialet avtar med økende temperatur, dvs. med tiden.
For å beregne trykkforholdene i beholderne er programsystemet PIA samt et spesialutviklet program PRESTEMP, benyttet. PIA er utviklet med utgangspunkt i Kameleon og er basert på samme numeriske modellering og metodikk som Kameleon. PIA er i utgangspunktet utviklet for å simulere trykkavlastning av prosessutstyr som befinner seg i risikoutsatte områder. Fokus for PIA ligger i veggmaterialets oppførsel og påkjenning ved trykkavlastning, idet dette ofte utsettes for svært store påkjenninger gjennom lave innvendige temperaturer som følge av rask trykkavlastning og ekspansjon, og samtidig kraftig utvendig oppvarming ved brann. Både den fluid- og termodynamiske utviklingen for multikomponente hydrokarbonblandinger i prosessutstyret, samt temperatur- og spenningsutvikling i materialveggene inngår i simuleringsmodellen. PIA er utviklet ved NTNU/Sintef Energiforskning AS, og bruksrettighetene ligger hos ComputIT. Programmet har vært anvendt av Sintef i en rekke studier av trykkavlastning, men også for eksempel for analyser av trykkoppbygging i rørledninger og for andre situasjoner. PRESTEMP er utviklet for denne studien og basert på de grunnleggende lover i termodynamikken. Det vekselvirker med den termodynamiske databasen NIST Chemistry WebBook (ref. 3).
I denne studien er trykkforholdene i den mest utsatte beholderen, dvs. på fremre vogn, beregnet. Brannlasten fører til en lokal oppvarming av stålmaterialet i den ene enden av vogna, og en global temperatur og trykkoppbygging i hele fluidet. Lokale temperaturvariasjoner i fluidet er ikke av signifikant betydning for trykkutviklingen i tanken.
Tabell 7.3 viser tilført varme til propantankene beregnet ved hjelp av Kameleon FireEx ved å summere varmeoverføringen over hele tankenes overflate. På grunn av vindforholdene mottar tankene noe forskjellig varme. For tilfelle A og B mottar fremre vogn mindre varme enn bakre vogn, mens i tilfelle C mottar fremre vogn mer varme enn bakre vogn. Dette siste skyldes oppvarming fra flammer på nedre del eller undersiden av fremre vogn i dette tilfellet (cfr. fig. 7.6), og har hatt en signifikant påvirkning på varmeoverføringen.
Tabell 7.3 Beregnet tilført varme til propanbeholderne
| Tilfelle | Massestrøm, m (g/s) | Utviklet varme (kW) | Tidspkt. (s) | Tilført tank på bakre vogn (kW) | Tilført tank på fremre vogn (kW) | Sum tilført (kW) | % av utviklet varme |
|---|---|---|---|---|---|---|---|
| A | 45 45 | 2087 2087 | 30 stasjonært | 99.5 96.0 | 65.7 59.7 | 165.2 155.7 | 7.9 7.5 |
| B | 90 90 | 4174 4174 | 30 stasjonært | 168.7 157.0 | 102.7 92.4 | 271.4 249.4 | 6.5 6.0 |
| C | 135 135 | 6261 6261 | 30 stasjonært | 217.3 208.2 | 311.9 280.1 | 529.2 488.3 | 8.5 7.8 |
Tabell 7.3 viser for øvrig at tankene til sammen mottar 6–8.5 % av den utviklede varme. Dette er meget realistiske verdier når en tar i betraktning flammenes størrelse, lokalisering og form.
En kan videre se at tankene mottar noe mindre varme etter at stasjonære forhold har inntrådt enn i begynnelse. Dette har sammenheng med at avstrålingen fra tankene øker med økende materialtemperaturer.
For trykkberegningene har vi lagt til grunn varmeoverføringen ved stasjonære forhold; for tilfelle A 59.7 kW, tilfelle B 92.4 kW, og tilfelle C 280.1 kW, som angitt i tabell 7.3. Vi har lagt de stasjonære varmefluksene til grunn fordi den transiente perioden, dvs. tiden før ståltemperaturen i gassområdet har nådd sin tilnærmede stasjonære tilstand, bare vil være 10–20 minutter.
Resultatene er vist i figur 7.10, der beregnet trykkutviklingen som funksjon av tid er fremstilt for de tre tilfellene.
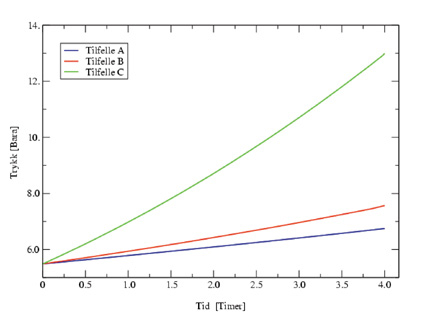
Figur 7.24 Beregnet trykkutvikling i propantank fremre vogn som funksjon av tid etter antennelse
Sammenhengen mellom temperatur og trykk er vist i figur 7.11.
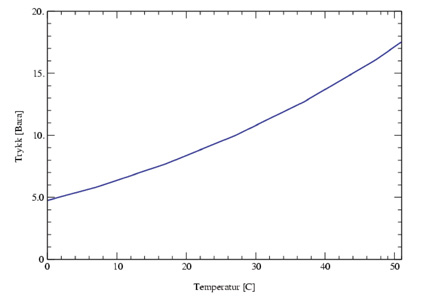
Figur 7.25 Fasekurve for propan
Trykket i beholderne vil være bestemt av væsketemperaturen. Lokalt høye materialtemperarturer i gassområdet vil i hovedsak ikke påvirke trykket på annen måte enn gjennom varmeoverføringen.
Brannvann ble tatt i bruk etter omtrent to timer, og det beregnede trykket er da hhv. 6.1 bara, 6.4 bara og 8.7 bara for de tre tilfellene. Dersom ikke brannvann var blitt tatt i bruk ville trykket ha fortsatt å øke. Det beregnede trykknivået etter 4 timer uten bruk av brannvann er 6.8 bara, 7.6 bara, og 13.0 bara hhv. for tilfelle A, B og C. Konsekvenser av dette er diskutert nærmere i kapitel 3.4.3.
7.3.4 Styrketeknisk analyse
7.3.4.1 Tankmaterialets styrkeegenskaper
Tankmaterialet betegnet StE47 (BH47) har en flytegrense på 470 N/mm2 .
Flytegrensen er temperaturavhengig og har den egenskap at den avtar med økende temperatur. Dette gjør seg gjeldende først og fremst ved temperaturer over ca. 300 °C.
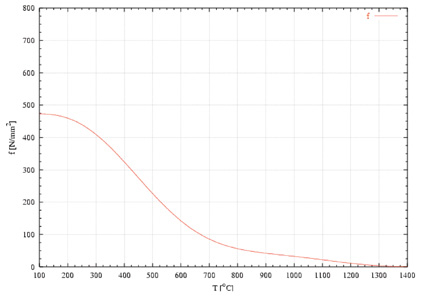
Figur 7.26 Flytegrensens variasjon med materialtemperaturen (typisk)
Figur 7.12 viser flytegrensens variasjon for et typisk stålmateriale tilsvarende det som er benyttet. Vi kjenner ikke eksakt forløpet for det angjeldende materiale, men vi antar at figur 7.12 karakteriserer temperaturavhengigheten godt nok, cfr. appendiks A «An estimation of the state of stress in the Lillestrøm gas tank».
Eksempelvis er flytegrensen sunket til 220 N/mm2 ved 500 °C, tilsvarende er reduksjon til 47 % av den opprinnelige (ved 20 °C). Ved 700 °C er flytegrensen sunket til ca 85 N/mm2 tilsvarende 18 % av den opprinnelige.
7.3.4.2 Tankenes dimensjonering
Tankene er konvensjonelt dimensjonert for å tåle et trykk på 25 bar overtrykk ved normal temperatur, altså med flytegrense for materialet på 470 N/mm2 . Det er på vanlig måte tatt hensyn til sikkerhetsfaktor og svekkelsesfaktor for sveiser.
Tankene består av en sylindrisk del og kuleformede endebunner. For den sylindriske delen beregnes strekk-membranspenningene etter følgende uttrykk
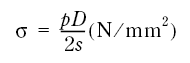
Figur 7.27
hvor
p = overtrykket i N/mm2
D = diameterne i mm
S = veggtykkelsen i mm
Her er D = 3000 mm og s = 12.2 mm.
Beholderens endebunner er utformet som kuleskall med krumningsradius R = 2400 mm. Strekk-membranspenningene i endebunnen beregnes av uttrykket
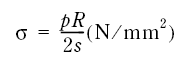
Figur 7.28
Her er R = 2400 mm og s = 13.1 mm.
Dette er de formler som normalt legges til grunn ved dimensjonering. Endebunnene er noe mer konservativt dimensjonert enn den sylindriske delen, bl.a. for å hensynta spenningene i overgangssonen mellom endebunnen og sylinderdelen.
7.3.4.3 Tankenes spenningssituasjoner under brannen
Det er tankenes endebunner som er utsatt for den største termiske belastningen fra brannen. Spesielt er det den fremre vogn, altså den tiltede vognen, som er mest utsatt fordi væskenivået er så lavt i den brannutsatte delen. Derfor vil områder av tanken her bli betydelig oppvarmet av brannen.
Det er tre spenningssituasjoner som er av interesse:
a: spenninger som oppstår på grunn av temperaturgradient gjennom veggmaterialet
b: spenninger på grunn av lokal termisk ekspansjon i de oppvarmede områder
c: spenninger på grunn av trykket inne i beholderen
Spenningssituasjonen a opptrer først og fremst ved store veggtykkelser. I dette tilfellet vil denne spenningen være av liten relativ betydning da beholderne kan betraktes som tynnveggede.
Spenningssituasjonen b vil under de riktige betingelser kunne føre til bukling av endebunnen.
Spenningssituasjonen c er den normale som er den vanlige dimensjonerende spenning.
Spenningssituasjonene b og c er utførlig drøftet i appendiks A, «An estimation of the state of stress in the Lillestrøm gas tank».
Konklusjonen av denne analysen er at det er membranspenningene som er kritiske og det er disse som blir lagt til grunn i det følgende.
Tabell 7.4 viser trykk- og spenningsutvikling i tanken på fremre vogn som funksjon av tid etter antennelse. Beregningene er gjennomført for lekkasjerate A: 45 g/s, B: 90 g/s, og C: 135 g/s. Det er lagt til grunn beregnet tilført varme, maksimal beregnet materialtemperatur, samt beregnet propantrykk.
Tabellen viser for øvrig flytekapasiteten be-stemt av beregnet maksimal materialtemperatur fra figur 7.12.
Videre vises kapasitetsutnyttelsen, dvs. forholdet mellom den maksimale membranspenningen og flytekapasiteten, angitt i %.
Figur 7.13 fremstiller resultatene grafisk. Vi ser her at lekkasjetilfelle C gir full kapasitetsutnyttelse etter i underkant av 3 timer. Dette er det tilfellet som vi etter en betraktning av de beregnede flammebilder har vurdert som det mest sannsynlige.
Sammenholdes dette med figur 7.14 som viser et bilde av fremre tank med en utbuling i det aktuelle området, en indikasjon på at flytegrensen har vært overskredet, underbygger dette en konklusjon om at brannutviklingen har vært i nærheten av den som er simulert i tilfelle C. Muligens har utstrømningsraten vært noe større.
Selv om en tar i betraktning at det i denne analysen er gjort beregninger av et meget komplekst fenomen, og at det derfor vil hefte usikkerhet ved beregningsresultatene, underbygges analysen en konklusjon om at situasjonen har vært meget alvorlig.
Det er viktig å ta i betraktning ved en videre vurdering at i første fase etter en utbuling vil en få en spenningsreduksjon fordi krumningsradien i det aktuelle området reduseres. Dette vil forsinke den videre utvikling, men situasjonen var alvorlig og vannavkjølingen startet i høy tid.
Tabell 7.4 Trykkutvikling og spenningsutvikling i fremre tankvogn som funksjon av tid etter antennelse
| Tilfelle | Tid (timer) | Tilført varme(kW) | Maks. temp (°C) | Trykk (bara) | Maks membran Spenning (N/mm2 ) | Flyte Kapasitet ved maks temp (N/mm2 ) | Kapasitetsutnyttelse % |
|---|---|---|---|---|---|---|---|
| A | 0 1 2 3 4 | 59.7 | 525 | 5.5 5.8 6.1 6.4 6.8 | 41.2 44.0 46.7 49.5 53.1 | 200 | 21 22 23 25 27 |
| B | 0 1 2 3 4 | 92.4 | 650 | 5.5 5.9 6.4 7.0 7.6 | 41.2 44.9 49.5 55.0 60.5 | 110 | 38 41 45 50 55 |
| C | 0 1 2 3 4 | 280.1 | 690 | 5.5 7.0 8.7 10.7 13.0 | 41.2 55.0 70.5 88.9 109.9 | 90 | 46 61 78 99 122 |
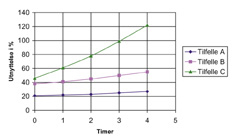
Figur 7.29 Flytekapasitetsutnyttelse i % som funksjon av tid etter antennelse

Figur 7.30 Fotografi av den mest utsatte endebunnen for tank på fremre vogn
7.3.5 Konklusjon
På basis av det ovenstående konkluderes følgende:
Med stor sannsynlighet har det vært en brannutvikling i nærhet av den som er simulert i tilfelle C, med en lekkasjerate på 135 g/s, eller kanskje noe høyere.
Når vi sammenholder beregninger og observasjoner og tar i betraktning usikkerheter, er det sannsynlig å anta at flytekapasiteten for beholdermaterialet i det brannutsatte området på fremre vogn ble overskredet etter ca. 2 timers brann.
Det var kritisk viktig å nedkjøle tankene med vann, og dette forhindret med stor sannsynlighet en videre utvikling mot katastrofe.
Dette var en alvorlig ulykke hvor i hovedtrekk de riktige katastrofehindrende tiltak ble iverksatt.
7.4 Analyse av alternative hendelsesforløp
7.4.1 Alternative hendelsesforløp
I det følgende har en analysert konsekvenser av en rekke alternative hendelsesforløp. Disse grupperes i tre problemområder:
Brannbelastning på vognene under andre ytre forhold, dvs forskjellige vindforhold, forskjellige lekkasjerater og ved annen initialtilstand i tankene.
Spredning av ikke antent gass under forskjellige vindforhold, og eventuell antennelse på et senere tidspunkt.
Fullstendig brudd på en beholder med momentant utslipp av all propan fra en tank, antennelse og dannelse av en såkalt «fireball».
7.4.2 Brannbelastning på fremre tankvogn ved andre vær- og lekkasjeforhold
7.4.2.1 Brannbelastning på fremre vogn
For problemområde 1 ovenfor er følgende alternative ulykkesscenarier definert:
Scenario D: som tilfelle C, dvs samlet lekkasjerate 135 g/s og vind 1.5 m/s, men med starttemperatur 20 °C i tankene
Scenario E: lekkasjerate 135 g/s, vind 15 m/s langs togvognene mot fremre vogn
Scenario F: lekkasjerate 1350 g/s, vind 1.5 m/s langs togvognene mot fremre vogn
Scenario G: lekkasjerate 1350 g/s, men vind 15 m/s langs togvognene mot fremre vogn
Alle brannene er simulert med Kameleon FireEx som beskrevet i kapitel 3.2.2, og resultatene er fremstilt på samme måte.
For scenario D er samme brann som for tilfelle C benyttet, mens det er de indre forhold i tanken som er endret. For beskrivelse av selve brannforløpet, avbildning av brannforløp, plott av beregningsresultater etc, henvises til figurene 7.6a-7.6d, samt 7.7c i kapitel 3.2.2.
Figurene 7.15 og 7.16 viser resultater for scenario E.
Figur 7.15a, b og c viser hhv. de maksimale temperaturene i flammen sett inn mot fremre vogn, den maksimale strålingsfluksen fra flammen inn på endebunnen på fremre vogn, og ståltemperaturene i den samme enden av fremre tank (som vender inn mot spalten mellom vognene). Figur 7.16 viser beregningsresultater sett fra siden slik at belastningen på sylinderdelen av fremre tank vises. Her er vist konsentrasjonen av propan som volumprosent, flammetemperatur, ståltemperatur, og maksimal strålingsfluks inn mot de viste flater. Der konsentrasjon av uforbrent propan vises på plottene indikerer dette at det ikke brenner i særlig grad i disse områdene og brannen er lokalisert på andre steder, og følgelig vil ikke disse områder være de mest utsatte med tanke på strålingsbelastning.
Figurene 7.17 og 7.18 viser tilsvarende som ovenfor for scenario F. Figurene 7.19 og 7.20 viser tilsvarende resultater for scenario G.
Figur 7.21 viser «ray-tracing» bilder, dvs bilder som avbilder flammene sett utenfra for de tre scenariene E, F og G.
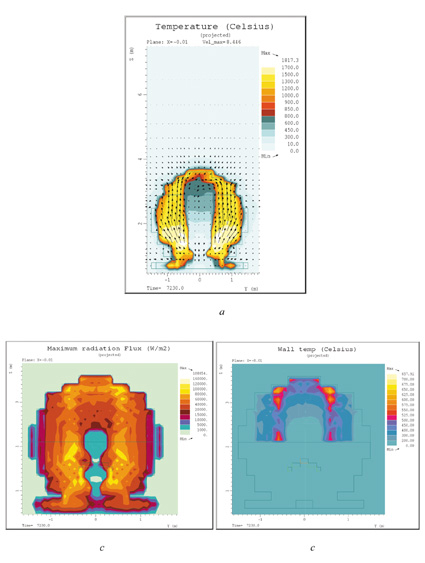
Figur 7.31 Beregningsresultater for endebunnen tilfelle E, 135 g/s, vind 15 m/s
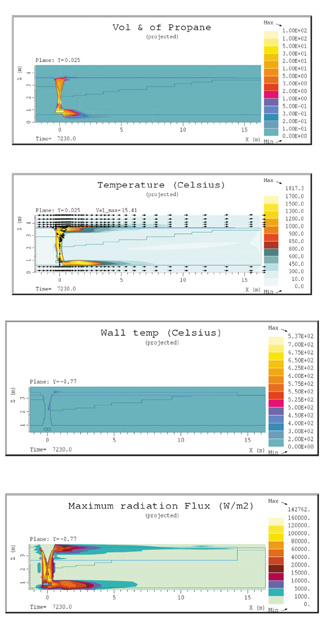
Figur 7.32 Beregningsresultater sett fra siden av fremre vogn tilfelle E, 135 g/s, vind 15 m/s
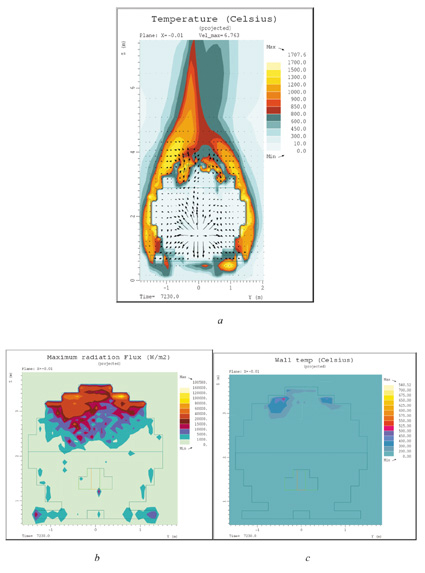
Figur 7.33 Beregningsresultater for endebunnen tilfelle F, 1350 g/s, vind 1.5 m/s
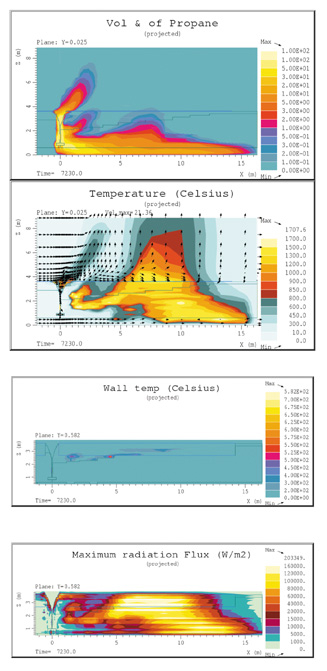
Figur 7.34 Beregningsresultater sett fra siden av fremre vogn tilfelle F, 1350 g/s, vind 1.5 m/s
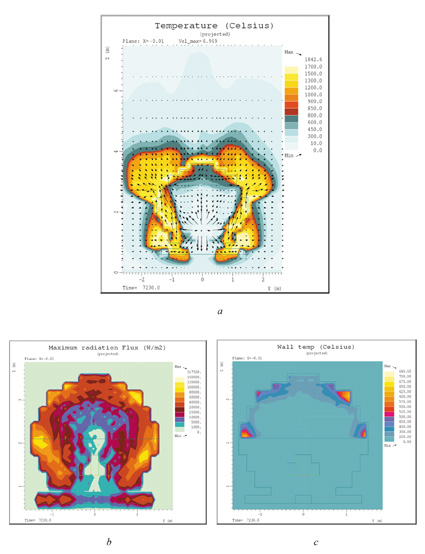
Figur 7.35 Beregningsresultater for endebunnen tilfelle G, 1350 g/s, vind 15 m/s
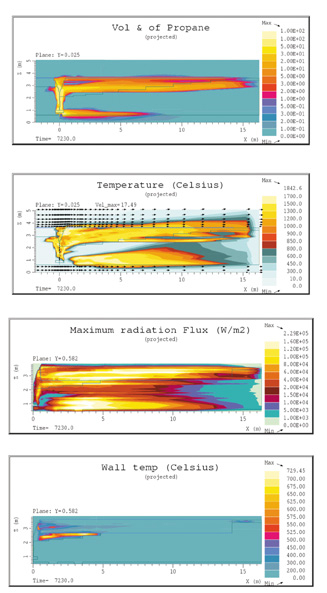
Figur 7.36 Beregningsresultater sett fra siden av fremre vogn tilfelle G, 1350 g/s, vind 15 m/s

Figur 7.37 Ray-tracing bilder av de beregnede flammene, scenario E, F og G
For scenario E som er samme situasjon som C, men med sterkere vind (15 m/s langs vogna i retning fremover), ser en at flammen legger seg ned langs fremre vogn og følger denne fremover, figur 7.15 og 7.16. Det ligger også en flammetunge i nedre kant av vogna bakover. Maksimalverdiene for strålingsfluks og ståltemperatur er litt lavere enn for tilfelle C, men den tilførte varmen er pga. flammens form og beliggenhet, betydelig større, 788 kW mot 280 kW.
Scenario F omhandler en lekkasjerate som er 10 ganger så stor som i basistilfellet, og liten vind, 1.5 m/s. Av figurene 7.17 og 7.18 kan en se at mellom vognene brenner det i mindre grad enn for de foregående tilfellene pga. høye propankonsentrasjoner og lite innblanding av luft i dette området. Dette fører også til at endebunnen er mindre utsatt mhp stråling og får også lavere ståltemperatur enn i tilfelle C. Imidlertid er denne flammen betydelig større, og strålingen både på oversiden og langs siden av sylinderdelen av tanken er betydelig større enn for tilfelle C. Flammen stiger dels rundt og opp pga. oppdriftskrefter kombinert med liten vind, og ligger dels på nederste del av beholderen lengst bort fra lekkasjepunktet. Den beregnede maksimale ståltemperaturen finner vi på sylinderdelen av tanken, i gassområdet rett nedenfor strålingsskjoldet. Strålingsskjoldet har for dette tilfellet en positiv virkning ved at strålingen til øvre del av tanken reduseres. Den tilførte varmemengden er imidlertid svært mye større enn for tilfelle C, 4610 kW mot 280 kW, og mye av varmen overføres i væskeområdet.
Scenario G er som scenario F, men med større vindhastighet, 15 m/s. Sammenliknet med scenario F brenner det her bedre mellom tankene, sannsynligvis på grunn av bedre innblanding av luft. Samtidig legger flammen seg langs sylinderdelen av tanken i hele dens lengde pga. den sterke vinden, og lite av flammen stiger opp. Den totale varmemengden som overføres til beholderen er 5439 kW, altså nesten 20 % mer enn med liten vind. Høyeste beregnede ståltemperatur er også her på sylinderdelen av tanken i gassområdet rett nedenfor strålingsskjoldet.
Tabell 7.5 viser en sammenstilling av resultater fra Kameleon FireEx beregningene etter at stasjonære forhold har innstilt seg. Tabell 7.6 gir en oversikt over beregnet varmemengde tilført beholderne.
Tabell 7.5 Karakteristiske resultater fra Kameleon FireEx beregningene
| Scenario | Lekkasjerate (g/s) | Vind (m/s) | Utviklet varme (kW) | Maks flamme-temperatur (°C) | Maks strålingsfluks inn mot fremre vogn (kW/m2 ) | Maks ståltemperatur tank fremre vogn (°C) |
|---|---|---|---|---|---|---|
| D | 135 | 1.5 | 6261 | 1682 | 130 | 690 |
| E | 135 | 15 | 6261 | 1817 | 109 | 658 |
| F | 1350 | 1.5 | 62610 | 1708 | 101 (203) | 541 (582) |
| G | 1350 | 15 | 62610 | 1843 | 118 (229) | 646 (731) |
Tallene i parentes i tabell 7.5 angir varmefluks og temperatur på den sylindriske delen av fremre vogn. De øvrige strålingsflukser og materialtemperaturer refererer til endebunnen på tanken på fremre vogn.
Tabell 7.6 Beregnet tilført varme til propanbeholderne
| Tilfelle | Masse strøm, m (g/s) | Utviklet varme (kW) | Tidspkt. (s) | Tilført tank på bakre vogn (kW) | Tilført tank på fremre vogn (kW) | Sum tilført (kW) | % av utviklet varme |
|---|---|---|---|---|---|---|---|
| D | 135 | 6261 | Stasjonært | 208 | 280 | 488 | 7.8 |
| E | 135 | 6261 | stasjonært | 338 | 788 | 1126 | 18.0 |
| F | 1350 | 62610 | stasjonært | 426 | 4610 | 5036 | 8.0 |
| G | 1350 | 62610 | stasjonært | 875 | 5439 | 6314 | 10.1 |
7.4.2.2 Trykk- og spenningsutvikling i fremre tank
I figur 7.23 er trykkutviklingen i fremre tank fremstilt som funksjon av tid etter antennelse. Likeledes er i tabell 7.7 gitt beregnet trykk og spenningsutvikling i fremre tank som funksjon av tid etter antennelse. Alle beregninger er utført på samme måte som beskrevet i kapitel 3.3 og 3.4 med inngangsdata som gitt i tabell 7.6.
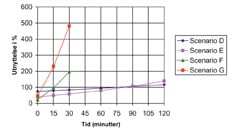
Figur 7.38 Flytekapasitetsutnyttelse i % som funksjon av tid etter antennelse
Tabell 7.7 Trykkutvikling og spenningsutvikling i fremre tankvogn som funksjon av tid etter antennelse
| Tilfelle | Tid (minutter) | Tilført varme (kW) | Maks. temp (°C) | Trykk (bara) | Maks membran spenning (N/mm2 ) | Flyte kapasitet ved maks temp (N/mm2 ) | Kapasitetsutnyttelse % |
|---|---|---|---|---|---|---|---|
| D | 0 30 60 90 120 150 180 | 280 | 690 | 8.3 9.3 10.2 11.3 12.4 13.6 14.9 | 66.9 76.0 84.3 94.3 104.4 115.4 127.3 | 90 | 74 84 94 105 116 128 141 |
| E | 0 30 60 90 120 | 788 | 658 | 5.5 7.6 10.2 13.3 16.9 | 41.2 60.5 84.3 112.7 145.6 | 105 | 39 58 80 107 139 |
| F | 0 15 30 | 4610 | 541 (582) | 5.5 13.2 25.6 | 41.2 111.8 (150.1) 225.3 (302.6) | 185 (155) | 22 60 (97) 122 (195) |
| G | 0 15 30 | 5439 | 646 (730) | 5.5 15.1 30.4 | 41.2 129.2 (173.4) 269.3 (361.6) | 115 (75) | 46 112 (231) 234 (482) |
Tallene i parentes i tabell 7.7 angir verdier knyttet til den sylindriske delen av fremre vogn. De øvrige verdiene refererer til endebunnen på tanken på fremre vogn.
Tabell 7.7 viser også flytekapasiteten bestemt av beregnet maksimal materialtemperatur på basis av figur 7.12. Videre vises kapasitetsutnyttelsen, dvs. forholdet mellom den maksimale membranspenningen og flytekapasiteten, angitt i %.
Av tabell 7.7 fremgår at for scenariene F og G er den sylindriske delen av fremre tank den mest utsatte. Her er de høyste ståltemperaturene beregnet og her er også dimensjoneringen noe svakere. For de øvrige scenariene er det endebunnen på fremre vogn på den siden hvor lekkasjen er, som er mest utsatt.
Figur 7.22 fremstiller resultatene grafisk.
For scenariene D og E vil flytekapasiteten ha blitt overskredet etter ca. 90 minutter, altså ca. 30 minutter før vannoverrislingen startet.
For scenariene F og G ville flytekapasiteten ha blitt overskredet etter hhv. ca 15 minutter og ca. 5 minutter. I virkeligheten ville kapasitetsoverskridelsen forsinkes sannsynligvis med ca. 10 minutter på grunn av transientene i temperaturutviklingen for stålmaterialet i gassområdet (cfr. kapitel 3.3).
Brudd vil inntreffe ved en høyere spenning enn flytespenningen. En kan regne med at brudd ville ha inntrådt innen ca. 20 minutter for scenario G. Dette er i samvar med internasjonale erfaringer. Det er vanskelig å tenke seg at en kunne ha forhindret katastrofe hvis scenario F eller G hadde opptrådt.
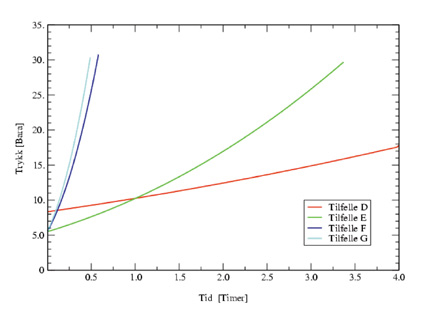
Figur 7.39 Beregnet trykkutvikling i propantank fremre vogn som funksjon av tid etter antennelse
7.4.3 Spredning av ikke antent gass med eventuelt senere antennelse
For problemområde 2 i kapitel 4.1 er følgende alternative ulykkesscenarier definert:
Scenario H: spredning av gass uten at gassen antennes. Som tilfelle C, dvs samlet lekkasjerate 135 g/s og vind 1.5 m/s. Vind i retning mot stasjonsbygningene
Scenario I: som H, men vindstille forhold
Scenario J: antennelse av scenario I etter ca. 3.5 timer
Alle simuleringene er gjennomført med Kameleon FireEx.
Figur 7.24 viser konsentrasjonen av propan rundt vognene og mot selve stasjonsområdet. Vinden blåser i retning av stasjonsbygningene, og gassen tynnes relativt fort ut som det også fremgår av figur 7.24. Generelt vil gassen tynnes mere ut med sterkere vind. Ved stasjonsbygningene er det beregnet gasskonsentrasjoner på 0.1 %–1 % av nedre flammegrense, noe som er altfor lavt til at gassen vil kunne brenne her. Nedre flammegrense (LEL) tilsvarer en propankonsentrasjon på 2.1 vol %.
Beregnede konsentrasjoner som tilsvarer nedre flammegrense eller større finnes bare i en kjegleformet sektor nedstrøms lekkasjepunktet i en utstrekning i lengderetning på ca. 30 m. Konsentrasjoner tilsvarende 20 % av LEL kan observeres ca 50–60 m nedtrøms lekkasjepunktet.
I figur 7.25 er vist de tilsvarende resultater for scenario I. Her er det vindstille og gassen sprer seg mer rundt lekkasjepunktet i alle retninger avhengig av høydeforskjeller i terrenget. Konsentrasjoner i området rundt LEL finnes for dette tilfellet i et noe større område, omtrent 60 m i utstrekning langs togvognene. Dette skyldes at gassen ikke tynnes ut i samme grad som for scenario H. Det er imidlertid viktig å merke seg at brennbare konsentrasjoner bare finnes i et tynt sjikt ned mot bakken, størrelsesorden 10 cm i området inntil vognene.
Gassen som har spredd seg i terrenget rundt toget i det vindstille tilfellet over en periode på ca. 3.5 timer, er i scenario J antent i forkant av fremre vogn. For at gassen i det hele tatt skal kunne brenne, må antennelsen skje i nærheten av vognene der gasskonsentrasjonen er høy nok. I løpet av svært få sekunder er den brennbare gassen oppbrent, og det innstiller seg en stasjonær flamme lik den for tilfelle C. Figur 7.26 viser gasskonsentrasjonene i området før antennelse, mens figur 7.27 viser tilsvarende en god stund etter at en brannen har stabilisert seg som tilfelle C. Den lokale, transiente, svært kortvarige brannen vil sannsynligvis ikke representere noen fare for vognene eller områdene rundt vognene, med mindre personer hadde oppholdt seg i sonen nært vognene.
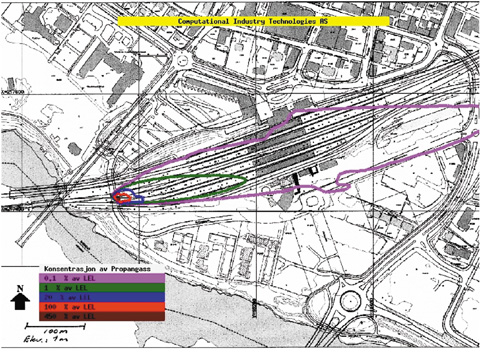
Figur 7.40 Beregnet konsentrasjon av propan i området rundt toget for scenario H
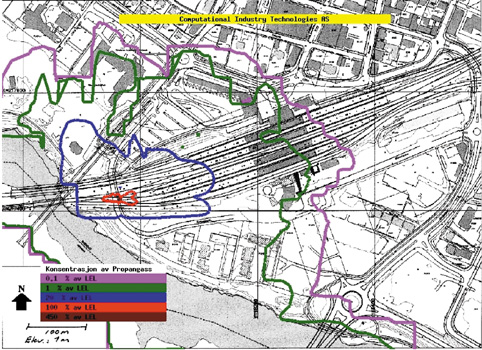
Figur 7.41 Beregnet konsentrasjon av propan i området rundt toget for scenario I
Ut fra scenariene H, I, og J kan følgende konklusjoner trekkes:
Uantent gass fra en lekkasje på 135 g/s vil tynnes fort ut og antakelig ikke representere noen stor risiko med tanke på antennelse og brannutvikling i områdene rundt lekkasjen
Dette betyr også at det sannsynligvis ville vært fordelaktig i den gitte situasjonen å slukke brannen og latt gassen strømme ut med den raten som eksisterte, mens de nødvendige tømmingstiltak ble iverksatt.
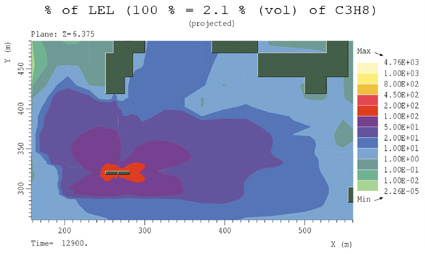
Figur 7.42 Gasskonsentrasjoner før antennelse, scenario J
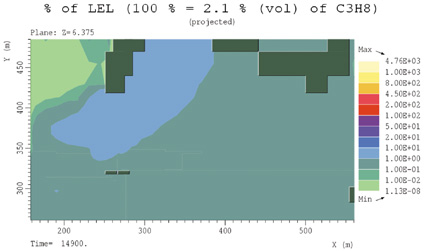
Figur 7.43 Gasskonsentrasjoner etter antennelse, scenario J
7.4.4 Fullstendig brudd på en beholder, fireball
Ved brudd på en tank vil gassen i løpet av meget kort tid, tilnærmet momentant, strømme ut. Utstrømningen vil både være i form av gas og væske. På grunn av det høye trykket i tanken, anslagsvis i området 15 bar, og tilsvarende høye temperaturer vil det skje en momentan fordampning av en del av væsken.
Dette vil føre til en effektiv blanding mellom luft og brensel. Ved antennelse vil en såkalt «fireball», ildkule, utvikle seg. Under utviklingen vil ildkulen bevirke en intens varmestråling.
I det følgende vises beregninger for ildkulen både ved hjelp av empiriske formler (ref. 4) og simuleringer med Kameleon FireEx.
7.4.4.1 Karakteristika for ildkule beregnet med empiriske formler
Ref. 4 gir følgende empiriske formler for ildkulen:
Maksimaldiameter: Dmaks = 6.48 M0.325 (m)
Der M (kg) er masse av opprinnelig brennbart materiale.
Varighet for ildkulen: t = 0.825 M0.26 (s)
Stråling fra ildkulen:
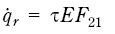
Figur 7.44
Hvor
τ = atmosfærens transmissivitet
E = σ T4 = stråling fra sort legeme (kW/m2 )
eller
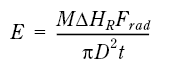
Figur 7.45
E er den gjennomsnittlige strålkingsfluks på ildkulens overflate under varigheten
Frad = andelen av utviklet varme som utstråles
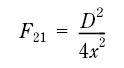
Figur 7.46
hvor
x er avstand (m) fra senter i ildkula til objekt
Vi setter inn følgende verdier for vårt tilfelle:
M = 43000 kg (en tank)
ΔHR = 46350 kJ/kg
Transmissiviteten, τ, er avhengig av luftfuktigheten, temperaturen på det utstrålende legeme, og aborberende partikler i atmosfæren. Vi antar:
τ = 0.65
Frad = 0.25
Dette gir:
Dmax = 208 m
t = 13.2 s
E = 278 kW/m2
Dette tilsvarer en overflatetemperatur for ildkulen
T = 1488 K = 1215 °C
Hvis en inkluderer transmissiviteten i overflatefluksen får en tilsynelatende overflatefluks
Ef = 181 kW/m2 ,
og tilsvarende overflatetemperatur
Tf = 1336 K = 1063 °C.
Strålingsfluksen som funksjon av avstanden fra sentrum i ildkulen, x, blir da
q = 2.0 106 /x2 (kW/m2 )
Dette gir følgende strålingsverdier:
x = 300 m qstr = 22.2 kW/m2
x = 400 m qstr = 12.5 kW/m2
x = 500 m qstr = 8.0 kW/m2
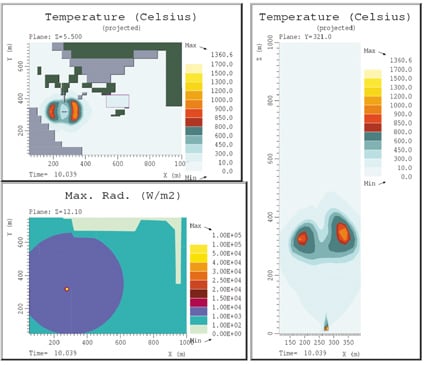
7.4.4.2 ldkuledannelse simulert med Kameleon FireEx
Det ble i simuleringene forutsatt at all propanen fra den ene tanken strømmet ut i løpet av 1 sekund.
Figurene 7.28, 7.29 og 7.30 viser ildkulens utvikling etter 5, 7, og 10 sekunder fra start på utslippet. Figurene viser ildkulens utvikling og stigning. Vi konstaterer at ildkulens diameter etter 7 sekunder er ca. 200 m sett ovenfra, altså omtrent det samme som gitt av formelen i kap. 4.4.1. Strålingsplottet i figurene viser strålingsnivået ved bakkenivå ved gitt tidspunkt. Vi beregner generelt noe lavere stråling enn hva formelen gir. Strålingen fra ildkulen er avhengig særlig av sotfordelingen på utsiden av ildkulen, altså av den tilsynelatende overflatetemperaturen. Dette kan variere med startbetingelsene, dvs. med utstrømningsforholdene fra beholderen. En kan derfor ikke eksakt fastlegge strålingsnivået på bakkenivået. Men en kan med sikkerhet fastslå at en slik ildkule vil frembringe en ekstremt høy varmestråling.
Det synes også som ildkulen brenner ut omtrent som etter formlene, dvs. etter ca. 10 sekunder.
I appendiks B er det gitt plott av resultater ved flere tidsnivå som angir hvordan ildkulen utvikler seg over tid.
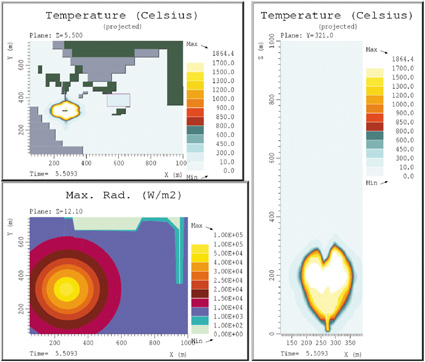
Figur 7.47
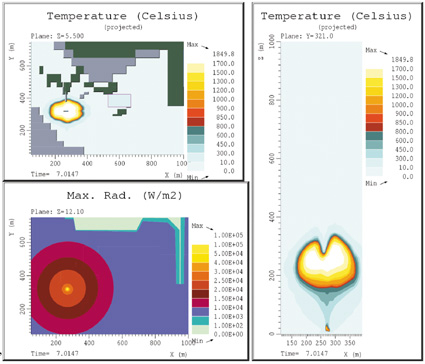
Figur 7.48
Figur 7.49
7.4.4.3 Konklusjoner vedr. ildkulen
Både formler og de numeriske simuleringene viser at det vil utvikles en formidabel ildkule hvis beholderen skulle eksplodere. En slik ildkule ville ha katastrofale virkninger for et betydelig område med utstrekning av størrelsesorden 1000 m.
Hvis begge beholderne skulle eksplodere, noe som ville være sannsynlig hvis den ene eksploderer, ville ulykkesomfanget være tilsvarende større.
7.5 Hovedkonklusjoner
Med stor sannsynlighet har det vært en brannutvikling i nærhet av den som er simulert i tilfelle C, med en lekkasjerate på 135 g/s, eller kanskje noe høyere.
Når vi sammenholder beregninger og observasjoner og tar i betraktning usikkerheter, er det sannsynlig å anta at flytekapasiteten for beholdermaterialet i det brannutsatte området på fremre vogn ble overskredet etter ca. 2 timers brann.
Det var kritisk viktig å nedkjøle tankene med vann, og dette forhindret med stor sannsynlighet en videre utvikling mot katastrofe.
Dette var en alvorlig ulykke hvor i hovedtrekk de riktige katastrofehindrende tiltak ble iverksatt.
Studien av alternative ulykkesscenarier viser at ulykken kunne ha fått et annet og mer omfattende og dramatisk omfang hvis lekkasjeraten hadde vært noe større og/eller hvis det hadde blåst sterkere vind langs vognene.
Simuleringene som ble utført for å studere konsekvensene av utstrømning av uantent propan, viser at uttynningen ville være meget kraftig slik at en sannsynligvis kan se bort fra eventuell eksplosjonsfare med tilhørende alvorlige konsekvenser.
I det aktuelle tilfelle viser gasspredningsberegningene at det sannsynligvis hadde vært fordelaktig å slukke brannen mens de nødvendige tømmingstiltak ble iverksatt.
Studien viser også at det er svært viktig å komme i gang med vannoverrisling, og at dette bør starte helst i løpet av den første halvtimen etter antennelse.
Hvis brannen hadde vært betydelig større enn i det aktuelle tilfelle er det tvilsomt om det ville være forsvarlig å starte vannoverrisling, eventeult slukning, da faren for eksplosjon og ildkuledannelse ville vært betydelig.
Analyse av ildkuleproblemstillingen viser at eksplosjon av en eller begge tankene ville ført til dannelse av en ildkule med katastrofale konsekvenser.
Det foreslås at det igangsettes et prosjekt hvor en med utgangspunkt i Kameleon FireEx simulerer en rekke forskjellige alternative hendelsesforløp for gasslekkasjer ved ulykker under transport av propan eller liknende på jernbane eller vei, for å fremskaffe et bredt underlag for å kunne treffe de riktige tiltak når ulykker av denne art inntreffer.
7.6 Referanser
«Bestemmelse av lekkasjeareal av 2 stk skadde propantanker på jernbanevogner», Rapport nr 23141-RT-0001-E02, Kjelforeningen Norsk Energi.
«Lekkasjeevaluering av skadde jernbanevogner for gasstransport»,Termek AS.
NIST Standard Reference Database 69 – February 2000 Release: NIST Chemistry WebBook (National Institute of Standard and Technology, USA).
«Guidelines for chemical process quantitative risk analysis», Center for chemical process safety of the American Institute of Chemical Engineers, 1989.
7.7 Appendiks A: Styrketeknisk analyse av propanbeholderen
An estimation of the state of stress in the Lillestrøm gas tank
Dr.ing. Thor Erik Hals Trondheim 09.08.2000
Introduction
A first order stress condition for the tank at low temperature, will consist of membrane stresses in large portions of the tank.
However, the edge conditions between the cylindrical shell and the elliptical end element, will give size to bending in a narrow edge zone. The additional bending stresses, superimposed on the membrane state, will give the criterion for determining the shell thickness in a normal working condition.
Membrane stresses due to inner pressure on end element
From photographs on the Lillestrøm location, it is seen that a local bulb is formed in the state of maximum fire temperature.
The final displacement of the bulb top (δmax ) and the diameter (2 so ) at the bulb’s bottom seem to be, respectively
δmax = 40 mm (2.1)
2 so = 450 mm (2.2)
The shape of the shell area around the bulb will be taken as a spherical form, having an approximate radius
ro = 2400 mm (2.3)
In a state of membrane stress equilibrium, one has the stresses
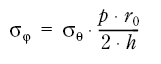
Figur 7.50
where
p = effective internal gas pressure
ro = approximate radius
h = shell thickness
In the following computations it will be assumed that p = 4, 6, 8 bar may be referred to temperature values
T = 600, 700, 800 °C respectively.
When h = 13 mm and
ro = 2400 mm
are inserted into Eq (2.4), one obtains
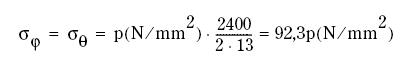
Figur 7.51
The results from Eq (2.5) are shown in the second entry of table 7.8.
Values of residual steel strength, according to fig 7.31, are given in the third entry of table 7.8. The last entry of table 7.8 yields the ratio strength/actual stress for increasing pressure and temperature.
Tabell 7.8 Tentative comparison between strength and actual stress
| P = 4 bar T ≈ 600 °C | P = 6 bar T ≈ 700 °C | P = 8 bar T ≈ 800 °C | |
|---|---|---|---|
| σϕ = σθ Eq. (2.5) | 36,9 N/mm2 | 55,4 N/ mm2 | 73,8 N/ mm2 |
| Residual steel strength, see fig. 2.1 | 150 N/mm2 | 83,3 N/mm2 | 55,6 N/mm2 |
| Strength/actual stress | 4,07 | 1,50 | 0,75 |
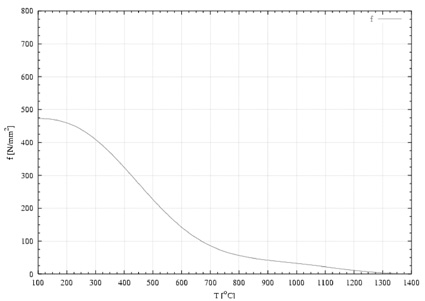
Figur 7.52 Residual steel strength
Membrane stresses due to gradient temperature strains
Description of temperature, Young’s modulus and thermal expansions coefficient
The temperature at a distance s from the bottom centre of the bulb, may be formulated
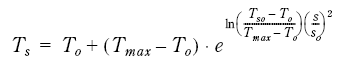
Figur 7.53
The various temperatures in Eq (3.1) are shown in fig. 3.32.
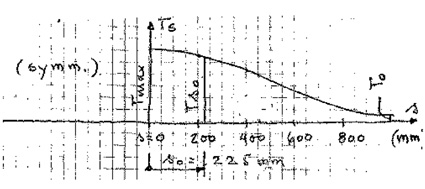
Figur 7.54 Temperature field of eq. (3.1). s=0 refers to bottom centre of bulb.
Young’s modulus is expressed as
ET = 2.1 × 105 (1 – 0,396 × Ts /600 °C) N/mm2 (3.2)
and the thermal expansion coefficient is taken in a similar form
αT = 1.1 × 105 (1+ 0,364 × Ts /600 °C) 1/°C (3.3)
In the following computations the limit temperature values will be taken as follows, see fig. 7.32.
Tmax = 600 °C at s = 0
Tso = 400 °C at s = so = 225 mm (3.4)
To = 5 °C at s = ∞
Edge displacement due to temperature Ts
The temperature displacement parallel to the tangent plane at the top of the bulb, will be
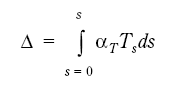
Figur 7.55
To obtain an axi-symmeteric problem, a slight tactical change of the computational model will be made. I.e. the deformed bulb is assumed to be located at the original top of the ellipsoidal shell element. Eq. (3.5) then yields, when upper integral limit is s = 1500 mm
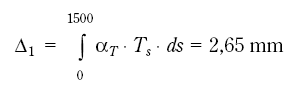
Figur 7.56
See fig. 7.33.
From the Geckeler theory for spherical shells, one now finds a homogeneous shell solution from two edge conditions at ϕ = π/2:
(i) δnom + Δ1 = 0 (3.7)
(ii) Vnom = 0
The displacement δ and the rotation V are connected with a shell state of edge forces at ϕ = ϕ0 this leads to
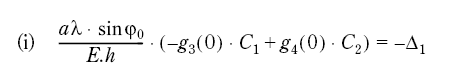
Figur 7.57
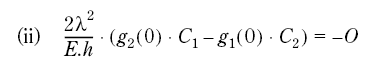
Figur 7.58
The various mathematical quantities are defined in fig. 7.34, part B and part C.
C1 and C2 in (i) and (ii) are constants of integration. Young’s modulus, E, and Poisson’s number, n, entering the Geckeler theory, will be given the low temperature values.
E = 2,1 · 105 N/mm2 (3.8)
ν = 0,3
The values in Eq (3.8) are chosen due to the fact that the edge zone is located at a considerable distance from the heated area of the bulb.
(ii) leads to
C2 = 0 (3.9)
as g2 (0)=0 and g1 (0)=1
(i) then gives the value for C1 when g3 (0)=1 is inserted:
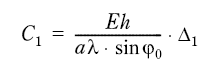
Figur 7.59
Finally, the membrane forces Nϕ and Nθ are found from fig. 7.34:
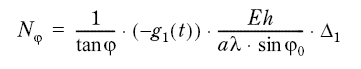
Figur 7.60
(3.11)
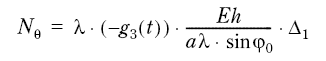
Figur 7.61
These forces have, in general, significant values close to the shell edge. However, the real bulb location referred to the axis, is at some angle
ϕbulb ≈ 70° = 1,22 rad (3.12)
This means that the argument t in the g-functions has values of special interest form zero to
t = λ(ϕo – ϕbulb )=λ(π/2 – 1,22) = λ × 0,35 rad (3.13)
The λ-quantity obtains the value:
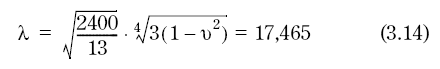
Figur 7.62
The Nϕ - and Nθ - forces in Eq (3.11) are divided by h=13 mm. One thus obtains the membrane stresses sϕT and sθT due to gradient temperature
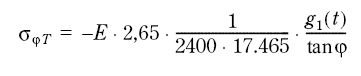
Figur 7.63
(3.15)
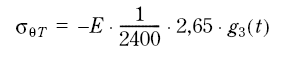
Figur 7.64
The interesting variations for ϕ and t will now be
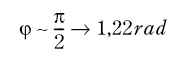
Figur 7.65
t ~ o → 6,11
The stresses in Eq (3.15) are listed in table 7.9.
Tabell 7.9 Stresses due to gradient temperature Ts
| σ = | t = | σϕT N/mm2 | σθT N/mm2 |
|---|---|---|---|
| π/2 | 0 | 0 | -110 |
| 1,4 | 3,0 | 0,11 | 4,60 |
| 1,3 | 4,7 | -0,0005 | 0,95 |
| 1,22 | 6,1 | -0,011 | -0,201 |
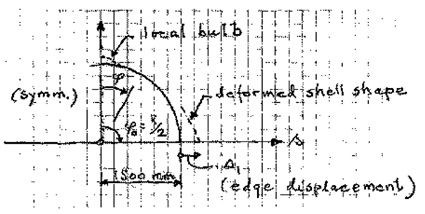
Figur 7.66 Deformed shell shape at the edge. Δ1 : edge displacement due to gradient temperature Ts .
Conclusions
The membrane stresses σϕT and σθT in table 7.9 have insignificant numerical values, compared to the σϕ - and σθ -stresses in table 7.8. Thus, the inner pressure p is definitely of major significance, when the shell structure’s safety is to be estimated.
The factors of safety from table 7.8 (strength/actual stress) show that the dangerous case exists, when the pressure p has a value between 6 and 8 bar.
This means that the approximate temperature interval from 700 °C to 800 °C is critical for the shell structure.
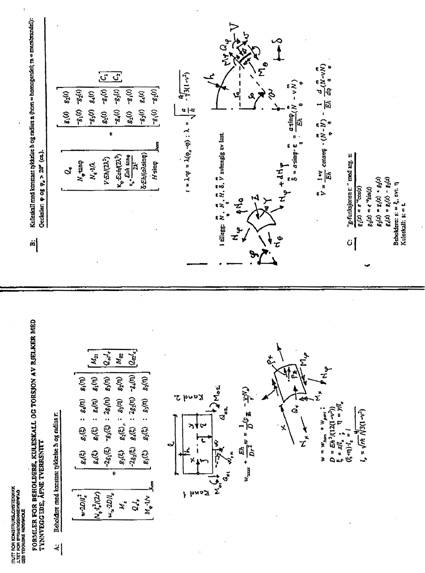
Figur 7.67 Cylindrical and spherical shell theory