4 Behandling av risiko i nytte-kostnadsanalyser
4.1 Innledning
Offentlige prosjekter vil i de aller fleste tilfeller strekke seg over flere år, og tilstander som inntreffer i fremtiden vil alltid være beheftet med en eller annen form for risiko. Lønnsomheten av et vegprosjekt avhenger bl.a. av trafikkutviklingen som igjen avhenger av bl.a. den makroøkonomiske utviklingen. I forbindelse med planleggingen av prosjektet vil det ikke være mulig å fastslå med sikkerhet hvordan disse størrelsene vil se ut om noen år. I dette kapitlet skal vi drøfte hvordan vi håndterer risiko i nytte-kostnadsanalyser. Vi starter i avsnitt 4.2 med å drøfte en del sentrale begreper i tilknytning til usikkerhet. I avsnitt 4.3 omtaler vi hvordan vi skal behandle risiko for et prosjekt der starttidspunktet er gitt, og prosjektet bare varer i én periode. I avsnitt 4.4 omtaler vi hvordan vi skal håndtere prosjekter som varer over flere perioder, mens vi i avsnitt 4.5 behandler valg av starttidspunkt. I avsnitt 4.6 drøfter vi kort bruk av såkalte sikkerhetsekvivalenter som et alternativ til risikojustering av diskonteringsrenten. Avsnitt 4.7 gir en kort oppsummering av tilrådingene i kapitlet.
4.2 Risiko - noen sentrale begreper
4.2.1 Forventede inntekter og kostnader
Vi starter med å illustrere beregning av forventede inntekter og kostnader ved hjelp av et stilisert eksempel. Anta at vi skal beregne lønnsomheten av de to veginvesteringene A og B. Vi antar at prosjektene bare varer i én periode, og at kostnader og prosjektinntekter påløper i hhv. begynnelsen og slutten av perioden.
Prosjekt A er en tunnel i et område med stabil trafikk. På grunn av den stabile trafikken kan vi med tilnærmet full sikkerhet si at tunnelen gir tidsinnsparinger som er verdt 110 mill. kroner. Det er 90 pst. sannsynlig at kostnadene blir på 80 mill. kroner, men med 10 pst. sannsynlighet vil vanskelige geologiske forhold gjøre at kostnadene blir på 280 mill. kroner.
Prosjekt B er en teknisk enkel vegutbedring der kostnadene blir 100 mill. kroner. Vegen har imidlertid et ustabilt trafikkgrunnlag, og verdien av tidsgevinstene ved vegutbedringen kan med like stor sannsynlighet bli 60 mill. kroner, 110 mill. kroner eller 160 mill. kroner avhengig av hvor godt det går i økonomien for øvrig.
Forventet verdi er definert som en veid sum der mulige utfall veies med de respektive sannsynlighetene for disse utfallene. I vårt tilfelle har begge prosjektene en forventet kostnad på 100 mill. kroner og en forventet prosjektinntekt på 110 mill. kroner. 1 Det er viktig å merke seg at den forventede kostnaden ikke er sammenfallende med den mest sannsynlige kostnaden. Det er altså den forventede prosjektkostnaden som skal benyttes i nytte-kostnadsanalysen, og ikke den mest sannsynlige kostnaden på 80 mill. kroner.
4.2.2 Systematisk og usystematisk risiko
Vi følger eksemplet fra punkt 4.2.1 videre, og vurderer hvordan usikkerheten påvirker nåverdien av prosjektene. Med en risikofri diskonteringsrente på 3,5 pst, er prosjektene like lønnsomme. Det er imidlertid en viktig forskjell mellom prosjektene. I prosjekt A er usikkerheten knyttet til geologien i området, slik at den faktiske kostnaden er uavhengig av hvordan det går i økonomien for øvrig. Også i andre prosjekter vil vi ha usikre kostnader som bare avhenger av spesifikke forhold i det enkelte prosjektet. For noen prosjekter vil de faktiske kostnadene bli lave, mens de i andre prosjekter vil bli høye. Siden det ikke er noen samvariasjon mellom kostnadene i de ulike prosjektene, vil imidlertid denne typen usikkerhet jevne seg ut når vi betrakter hele porteføljen av prosjekter. Dette betegnes usystematisk risiko, og medfører ikke at vi bør øke avkastningskravet til prosjektet.
I prosjekt B er verdien av tidsgevinstene knyttet til hvor godt det går i økonomien for øvrig. Prosjektet er dermed risikabelt også når vi betrakter hele porteføljen av prosjekter i samfunnet. Vi sier at det er systematisk risiko knyttet til prosjektet, slik at avkastningskravet til prosjektet bør økes. 2 Selv om både forventede kostnader og forventede inntekter er like for de to prosjektene, kan vi altså fastslå at prosjekt A er mer lønnsomt enn prosjekt B. Hvor mye vi bør øke avkastningskravet for prosjekter med systematisk risiko, er tema for neste avsnitt. I boks 4.1 har vi også gitt et enkelt eksempel på hvordan vi beregner forventede verdier og neddiskonterer dem med en risikojustert rente. Eksemplet viser også hvordan vi kan benytte sensitivitetsanalyser for å vurdere hvor stor betydning usikkerhet har for nåverdien av et prosjekt.
Boks 4.1 Boks 4.1 Forventede verdier og sensitivitetsanalyse
Anta at myndighetene vurderer å bygge en ny kortbaneflyplass i A-by. Det er en del usikkerhet knyttet til investeringskostnaden som påløper i år 0. Usikkerheten vurderes imidlertid i hovedsak som usystematisk. Etter en analyse av ulike kostnadskomponenter kommer vi fram til følgende sannsynlighetsfordeling for kostnadene (inkl. skattekostnad):
| Sannsynlighet | 0,1 | 0,2 | 0,2 | 0,2 | 0,2 | 0,1 |
| Kostnad (mill. Kroner) | 125 | 150 | 175 | 225 | 250 | 275 |
Forventet kostnad blir dermed:
K = 0,1.125 + 0,2.150 + 0,2.175 + 0,2.225 + 0,2.250 + 0,1.275 = 200
Vi gjør en grov analyse av de årlige nettoinntektene, og antar at de med like stor sannsynlighet kan bli «lave», «middels» eller «høye» avhengig av hvor godt det går i økonomien ellers. Vi får følgende sannsynlighetsfordeling for netto prosjektinntekt pr. år (inkl. verdien av økte skatteinntekter):
| Sannsynlighet | 1/3 | 1/3 | 1/3 |
| Netto inntekt (mill. Kroner) | 8 | 12 | 16 |
Forventet netto inntekt pr. år blir dermed:
I = 1/3.8 + 1/3.12 + 1/3.16 = 12
Prosjektet er konjunkturfølsomt, og vi benytter en diskonteringsrente på 8 pst. Dersom vi som en forenkling antar at prosjektet er evigvarende, får vi følgende nåverdikalkyle:

Prosjektet er dermed samfunnsøkonomisk ulønnsomt.
Vi kan også lage en enkel sensitivitetsanalyse for å finne ut hvor lave kostnadene må være for at prosjektet skal være lønnsomt (for gitt fordeling av inntektene):
NV = - K + 150 = 0 ⇒ K = 150
Fra sannsynlighetsfordelingen for kostnader ser vi dermed at det bare er 30 pst. sannsynlighet for å få så lave kostnader at prosjektet i ettertid viser seg å bli lønnsomt dersom inntektene blir som forventet.
På samme måte kan vi vurdere hvor høye inntektene må være for at prosjektet skal være lønnsomt (for en gitt fordeling av kostnadene):
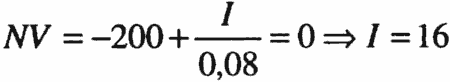
Fra sannsynlighetsfordelingen for inntekter ser vi at vi må ha høykonjunktur i alle fremtidige perioder for å få prosjektet lønnsomt dersom kostnadene ikke blir lavere enn forventet.
Eksemplet ovenfor gir en svært enkel illustrasjon på bruken av sensitivitetsanalyser. For en mer omfattende drøfting av dette temaet viser vi til kapittel 10 i Brealey og Myers (1996).
4.3 Risikojustering i praksis
Samfunnsøkonomisk relevant risiko for et prosjekt avhenger av graden av samvariasjon mellom prosjektavkastningen og nasjonalinntekten. Et samferdselsprosjekt vil f.eks. ha høyere trafikk, og dermed høyere avkastning, når det er høy aktivitet ellers i økonomien. Det er imidlertid vanskelig å måle hvilke risikopremier vi skal benytte for ulike prosjekter. Som en tilnærming kan det derfor være hensiktsmessig å benytte informasjon fra aksjemarkedet. Vi antar dermed at de risikopremiene vi kan observere i aksjemarkedet er representative for de risikopremiene vi bør benytte i en samfunnsøkonomisk analyse.
Data fra aksjemarkedet gir grunnlag for å finne risikojusterte avkastningskrav for prosjekter med ulik risiko. Den vanligste modellen å benytte er den såkalte kapitalverdimodellen, som uttrykker det risikojusterte avkastningskravet for prosjektet som summen av en risikofri rente og et risikotillegg. Størrelsen på risikotillegget for prosjektet avhenger av risikotillegget for markedsporteføljen og den relevante risikoen for prosjektet. Den relevante risikoen for prosjektet avhenger på samme måte som i avsnitt 4.2 av samvariasjonen mellom avkastningen på prosjektet og avkastningen på markedsporteføljen. Vi tar derfor bare hensyn til den delen av prosjektrisikoen som ikke forsvinner ved diversifisering (systematisk risiko). Kapitalverdimodellen og bruk av informasjon fra aksjemarkedet er nærmere drøftet i kapittel 9 i NOU 1997: 27.
For større prosjekter eller for grupper av prosjekter med tilnærmet samme risiko, bør risikojusterte avkastningskrav estimeres særskilt. For mindre, enkeltstående prosjekter kan det imidlertid være lite hensiktsmessig å beregne egne risikotillegg. På grunnlag av historiske risikopremier i aksjemarkedet foreslår vi å benytte inndelingen i tabell 4.1 når det ikke gjøres særskilte analyser. For prosjekter med risikotillegg på 4,5 pst., 2,5 pst. og 0,5 pst. innebærer dette at vi neddiskonterer forventet prosjektoverskudd med en diskonteringsrente på hhv. 8 pst., 6 pst. og 4 pst. når risikofri rente er lik 3,5 pst. 3
Tabell 4.1 Risikotillegg
| Prosjekttype | Risikotillegg |
| Prosjekter med om lag samme risiko som et gjennomsnittlig prosjekt finansiert i aksjemarkedet (f.eks. investeringer i kraftproduksjon og konjunkturfølsomme samferdselsinvesteringer) | 4,5 pst. |
| Prosjekter med middels risiko (f.eks. investeringer i kraftnett og kollektivtrafikkinvesteringer) | 2,5 pst. |
| Prosjekter med lav risiko (f.eks. investeringer i helse, aldershjem og grunnskoler) | 0,5 pst. |
| Offentlig forretningsdrift i direkte konkurranse med private aktører | Som tilsvarende private bedrifter |
For å kunne benytte inndelingen ovenfor, trenger vi noen tommelfingerregler for hvilket risikotillegg ulike prosjekter bør ha. Her er det to viktige forhold å ta hensyn til:
For det første bør vi vurdere hvor følsomme inntektene fra prosjektet er for samlet inntekt i økonomien, dvs. hvor konjunkturfølsomme de er. Høy konjunkturfølsomhet tilsier et høyt risikotillegg, mens prosjekter der nytten i hovedsak avhenger av f.eks. demografiske forhold bør ha et lavt risikotillegg.
For det andre har kostnadsstrukturen betydning for risikoen ved prosjektet. Et prosjekt blir mindre risikabelt dersom mye av kostnadene er variable slik at prosjektomfanget kan varieres i takt med etterspørselen. Generelt må det utøves en del skjønn for å plassere et prosjekt i riktig risikoklasse. Eksemplene i tabell 4.1 må også bare leses som en relativt grov vurdering av hvilke prosjekter som hører hjemme i hvilke klasser. 4
Høy konjunkturfølsomhet og andelen faste kostnader er også sentrale størrelser dersom vi skal estimere risikojusterte avkastningskrav. Vi går ikke videre med dette, men henviser til kapittel 9.4 i Brealey og Myers (1996) og de henvisningene som er gitt der. 5
4.4 Prosjekter som varer over flere perioder
De fleste prosjekter varer mer enn én periode, og vi må derfor ta stilling til om dette har betydning for det risikotillegget som bør benyttes. Det er vanlig å anta at risikoen i et prosjekt øker med avstanden i tid, slik at kostnader og inntekter som inntreffer i fjern fremtid, skal korrigeres mer enn dem som inntreffer den første tiden etter at prosjektet er iverksatt. Intuisjonen bak dette er at en vet mest om hvilke tilstander som inntreffer i nær fremtid, mens det er mer usikkert hvilke tilstander som inntreffer senere.
Det kan i denne sammenhengen være naturlig å ta utgangspunkt i bruk av en konstant, risikojustert diskonteringsrente. Dersom vi forutsetter at risikofri rente ikke vokser over tid, innebærer bruk av en konstant risikojustert diskonteringsrente en antagelse om at lønnsomheten i prosjektet er like utsatt for systematisk risiko i alle enkeltperiodene. Risikojustert diskonteringsrente kompenserer imidlertid bare for risikoen en bærer pr. periode. Dette innebærer at den samlede risikoen vil øke i takt med avstanden fra beslutningspunktet. For mange offentlige prosjekter er dette en rimelig antakelse. Vi vil derfor som en hovedregel anbefale at prosjektanalytikeren tar utgangspunkt i en konstant risikojustert diskonteringssats.
For enkelte prosjekter er det ikke rimelig å anta at prosjektet er like utsatt for systematisk risiko i alle enkeltperiodene. Dette kan f.eks. gjelde for investeringer der lønnsomheten er avhengig av internasjonale miljøavtaler. Når en miljøavtale er inngått og konsekvensene av den er kjent, vil deler av risikoen i prosjektet være oppløst. Denne typen risiko omtales ofte som milepælsrisiko, mens den resterende risikoen i prosjektet omtales som driftsrisiko. Milepælsrisikoen oppløses typisk relativt tidlig i prosjektet, mens driftsrisikoen oppløses gradvis over hele prosjektets levetid. I tilfeller hvor det er rimelig å anta at det er et betydelig innslag av milepælsrisiko, bør en ta hensyn til denne i forbindelse med risikojustering av prosjektet. Dette kan f.eks. gjøres ved at en opererer med et risikotillegg fram til milepælsrisikoen forventes å være oppløst, og et annet risikotillegg for kontantstrømmer som kommer senere. Bruk av ulike risikotillegg er illustrert i boks 4.2 i avsnitt 4.5.
4.5 Irreversibilitet og alternativkostnaden ved tapt opsjonsverdi
Så langt i dette kapitlet har vi lagt til grunn at et prosjekt er lønnsomt dersom risikojustert nåverdi er større enn null. Dersom investeringen er irreversibel, er imidlertid ikke en positiv risikojustert nåverdi lenger tilstrekkelig til å fastslå at prosjektet er lønnsomt. Utover positiv risikojustert nåverdi kan det i slike tilfeller oppstå en alternativkostnad som er verdien av å vente fremfor å gjennomføre prosjektet straks.
Alternativkostnaden ved tapt beslutningsfleksibilitet henger sammen med at en i noen tilfeller kan øke prosjektets forventede nåverdi ved å utsette iverksettelsen. Siden muligheten til å velge iverksettelsestidspunkt er å betrakte som en opsjon, omtales alternativkostnaden ved å iverksette prosjektet straks som tapt opsjonsverdi. Dersom prosjektet iverksettes, er opsjonen brukt opp. Opsjonens verdi er ofte knyttet til mulighetene for å utnytte ny informasjon ved å utsette prosjektet. I andre tilfeller er verdien knyttet til at nettoinntekten fra prosjektet øker over tid, slik at rentegevinsten ved å utsette investeringen kan oppveie de inntektene vi går glipp av ved senere oppstart.
I praksis beregner vi som oftest tapt opsjonsverdi ved å beregne nåverdien av prosjektet for ulike gjennomføringstidspunkter, jf. boks 4.2 og avsnitt 6.6. Vi kan derfor se på et prosjekt med ulike mulige gjennomføringstidspunkter som flere gjensidig utelukkende prosjekter, der vi skal velge det med høyest risikojustert nåverdi. 6
Boks 4.2 Boks 4.2 Milepælsrisiko og valg av oppstarttidspunkt
Anta at myndighetene vurderer å bygge ut et prosjekt for alternativ energiforsyning. Investeringskostnaden for prosjektet er 180 mill. kroner. Samtidig er flere land i ferd med å inngå en internasjonal miljøavtale som vil påvirke lønnsomheten av prosjektet. Dersom avtalen blir inngått, gir energikilden en samfunnsøkonomisk inntekt det første året på 25 mill. kroner, mens inntekten bare er 16 mill. kroner dersom det ikke blir inngått noen slik avtale. Sannsynligheten for at det blir en avtale anslås til 0,4. Under enhver omstendighet er imidlertid den samfunnsøkonomiske risikoen høy det første året, og myndighetene vurderer det som rimelig med en diskonteringsrente på 8 pst.
I senere år antar vi at prosjektet vil gi en evigvarende nettoinntekt på 12,5 mill. kroner med en avtale og 8,0 mill. kroner uten en avtale. Uavhengig av om det blir en avtale antar myndighetene at den systematiske risikoen for prosjektet er lavere fra og med det andre året, fordi virkningene av forhandlingsresultatet er fullt ut reflektert i markedet. Etter nærmere analyse fastsettes det en diskonteringsrente på 5 pst. for alle senere år.
Vi beregner først nåverdien av prosjektet gitt at vi må investere med en gang. I nåverdiberegningen må vi ta hensyn til at vi skal benytte ulike diskonteringsrenter før og etter at milepælsrisikoen knyttet til avtalen er endelig oppløst:
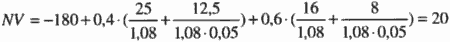
En annen mulighet er å utsette prosjektet til vi er sikker på om det er blitt en avtale. Den neddiskonterte verdien av netto kontantstrøm er lavere enn investeringsbeløpet dersom det ikke blir noen avtale (8/0,05=160), og vi vil derfor bare investere dersom det blir en avtale. Nåverdien regnet tilbake til i dag blir dermed:
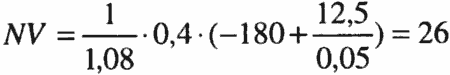
Det er dermed lønnsomt å utsette prosjektet for å ta hensyn til ny informasjon som gjør at milepælsrisikoen blir oppløst.
4.6 Sikkerhetsekvivalenter 7
I avsnittene ovenfor har vi håndtert usikkerhet ved å risikojustere diskonteringsrenten. Et alternativ er å justere ned kontantstrømmen samtidig som vi benytter en risikofri diskonteringsrente. Det nedjusterte kontantbeløpet i hver periode betegner vi sikkerhetsekvivalenten til det usikre kontantbeløpet. Mer presist definerer vi sikkerhetsekvivalenten i hver periode som det minste sikre beløpet vi er villige til å bytte den usikre netto prosjektinntekten med.
Bruk av sikkerhetsekvivalenter skal gi samme nåverdi som bruk av risikojustert diskonteringsrente. 8
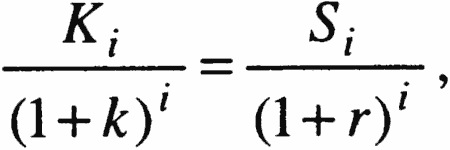
Det kan imidlertid i enkelte sammenhenger være en fordel å benytte sikkerhetsekvivalenter, for dermed å få fram mer eksplisitt hvordan usikkerhet påvirker verdien av kontantstrømmene. For en nærmere drøfting av sikkerhetsekvivalenter, viser vi til kapittel 9 i Brealey og Myers (1996).
4.7 Oppsummering
På grunnlag av drøftingen ovenfor kan vi oppsummere en stikkordsmessig prosedyre for håndtering av risiko i nytte-kostnadsanalyser:
Finn mulige utfall for inntekter og kostnader. Fastsett sannsynligheter for de ulike utfallene. Husk å ta med alle tenkelige utfall, også ekstreme utfall som opptrer med lav sannsynlighet.
Beregn forventet verdi.
Plasser prosjektet i en risikoklasse eller foreta eventuelt en særskilt vurdering av risikoen i prosjektet. Husk at det bare er den systematiske risikoen som har betydning for risikojusteringen. Konjunkturfølsomhet og andel faste kostnader er viktige ledetråder for å fastsette risikojustert diskonteringsrente (ev. sikkerhetsekvivalenter).
Vurder om prosjektet bør ha samme risikojusterte diskonteringsrente i hver periode. Innslag av milepælsrisiko tilsier bruk av ulike diskonteringsrenter i ulike perioder.
Vurder om prosjektet bør igangsettes nå, eller om det bør utsettes.
Fotnoter
De forventede verdiene fremkommer som hhv. 0,9 . 80 + 0,1 . 280 = 100 og 1/3 . 60 + 1/3 . 110 + 1/3 . 160 = 110
Vi kan også ha usystematisk risiko på inntektssiden av et prosjekt. Bruk av en veg kan f.eks. avhenge av om det er godt eller dårlig vær. På samme måte kan kostnadsrisiko være systematisk, f.eks. fordi lønnskostnader blir høyere når det går godt i økonomien.
I alle risikoklassene får vi dermed et tillegg til risikofri rente. Det er imidlertid i prinsippet mulig at avkastningen på enkelte prosjekter er negativt korrelert med nasjonalinntekten, og slike prosjekter bør i så fall ha et lavere avkastningskrav enn den risikofrie renten. Et mulig eksempel kan være investeringer for å gjennomføre arbeidsmarkedstiltak, der avkastningen trolig vil være størst når det er lavkonjunktur.
Se også Johnsen (1996) som anslår avkastningskrav for statlig eiet forretningsdrift.
Som det fremgår av drøftingen til Brealey og Myers (1996), unngår vi ikke å utvise skjønn også når vi estimerer avkastningskrav.
Fremgangsmåten i boks 4.2 og avsnitt 6.6 er ikke helt korrekt. Under usikkerhet må vi eksplisitt verdsette den aktuelle opsjonen for å få et helt riktig resultat. For en drøfting av verdsetting av opsjoner viser vi til Brealey og Myers (1996), kapitlene 20 og 21.
Dette avsnittet er ikke nødvendig å lese for å få sammenheng i kapitlet.
Med samme diskonteringsrente i alle perioder har vi dermed for periode i at (se figur i avsnitt), der K er forventet kontantstrøm, S er det sikkerhetsekvivalente beløpet, k er risikojustert diskonteringsrente og r er risikofri rente.